Matrix solution sensitivity to right side change (ill-conditioned matrix)

First solve the following system of linear equations

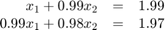
$\begin{array}{rcl} x_1 + 0.99x_2 &=& 1.99 \\ 0.99x_1 + 0.98x_2 &=& 1.97 \end{array}$

by solving the matrix system 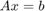$Ax=b$ , where

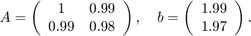
$A = \left( \begin{array}{cc} 1 & 0.99 \\ 0.99 & 0.98 \end{array} \right), \quad b = \left(\begin{array}{c}1.99 \\ 1.97\end{array}\right).$

A = [1 0.99;0.99 0.98];
b = [1.99;1.97];
x = A\b

Now consider a different RHS,

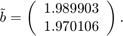
$\tilde{b} = \left(\begin{array}{c}1.989903 \\ 1.970106\end{array}\right).$

bt = [1.989903;1.970106];
xt = A\bt

xt =

   2.999999999999532
  -1.020299999999527

We can see that a small relative change in the right hand side

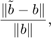
$\frac{\Vert \tilde{b}-b \Vert}{\Vert b \Vert},$

results in a large relative change in the solution

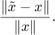
$\frac{\Vert \tilde{x}-x \Vert}{\Vert x \Vert}.$

fprintf('Relative change in RHS:      %g\n', norm(b-bt)/norm(b));
fprintf('Relative change in solution: %g \n ', norm(x-xt)/norm(x));

Relative change in RHS:      5.13123e-05
Relative change in solution: 2.01018