Forward Euler for ODE
We solve the ordinary differential equation
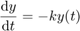
with initial conditions 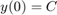 ,
,  , on the interval
, on the interval ![$(0, T]$](example4_eq14844194908659035275.png) ,
, 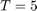 , and concentration
, and concentration 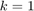 using forward Euler with timestep size
using forward Euler with timestep size 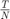 ,
, 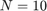 .
.
We note, that this equation has the known analytical solution
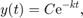
so we can compare to the numerical result.
N = 10; % interval [0,T] discretized with N+1 points C = 10; % value C (0) T = 5; % maximum time k = 1; % concentration h = T/N; % the step size h, we consider equi-distance division nC = C*ones(N+1,1); % numerical solution aC = C*ones(N+1,1); % analytical solution for i=1:N nC(i+1) = (1-k*h)*nC(i); aC(i+1) = C * exp(-k*h*i); end x = 0:h:T; % x-axis values plot(x,aC,'r-o','LineWidth',2); hold on; plot(x,nC,'b-o','LineWidth',2); hold on; legend('analytical solution', 'numerical solution');
