Question 5

Contents

5(a) - First order system

The second order system for the linear oscillator

$x'' + ax' + bx = c \cos(\omega t),$

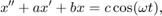
can be written as the first order system

$x'(t) = \left( \begin{array}{c} x_2 \\ -bx_1-ax_2+c\cos(\omega t) \end{array} \right).$

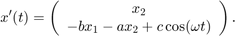
5(b) - Explicit solution

For 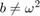$b\neq\omega^2$:

$\begin{array}{rl} x_1(t) &= K_1 \cos(\sqrt{b} t) + K_2 \sin(\sqrt{b} t) + c \frac{\cos(\omega t)}{b-\omega^2} \\ x_2(t) &= \sqrt{b}(-K_1\sin(\sqrt{b}t)+K_2\cos(\sqrt{b}t))-c\frac{\omega\sin(\omega t)}{b-\omega^2} \end{array}$

For 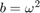$b=\omega^2$ (resonance case):

$\begin{array}{rl} x_1(t) &= K_1 \cos(\omega t) + K_2 \sin(\omega t) + C \frac{t\sin(\omega t)}{2\omega} \\ x_2(t) &= x_1'(t) \end{array}$

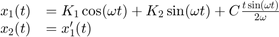
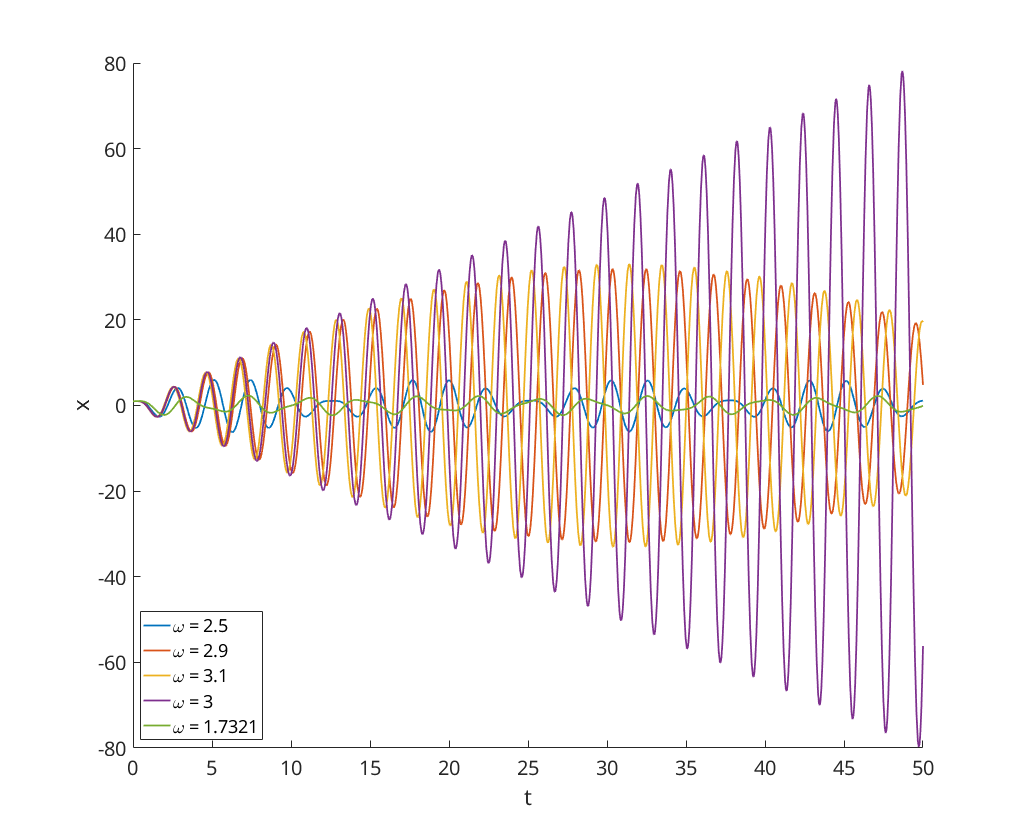
5(c) - Numerical Experiments

function q5_solution

figure;
hold on;
for omega=[2.5,2.9,3.1,3,sqrt(3)]
    [t,x] = ode23(@(t,x)oscillator(t,x,omega), [0, 50], [1, 0]);
    plot(t, x(:,1), 'DisplayName', ['\omega = ' num2str(omega)]);
end
xlabel('t');
ylabel('x');
legend('Location','SouthWest');

Modified oscillator function

Modified version of oscillator.m to allow $\omega$ to be passed as arg

end
function y = oscillator(t, x, omega)
% OSCILLATOR Right hand side for harmonic oscillator equation:
%
% x_1' = x_2
% x_2' = -b x_1 - a x_2 + c cos(\omega t)

a = 0;
b = 9;
c = 10;

A = [0 1; -b -a];
r = [0; c*cos(omega*t)];

y = A*x + r;

end

Published with MATLAB® R2023a