Question 1 - Cat & Mouse
We simulate the cat's position  in the Cat & Mouse system for
in the Cat & Mouse system for 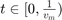 by the ODE system:
by the ODE system:
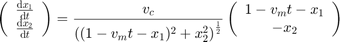
where 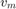 are
are 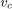 are the mouse's and cat's velocities, respectively. The initial starting position of the mouse is given by
are the mouse's and cat's velocities, respectively. The initial starting position of the mouse is given by 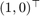 and the cat by
and the cat by 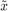 .
.
Contents
1(a)
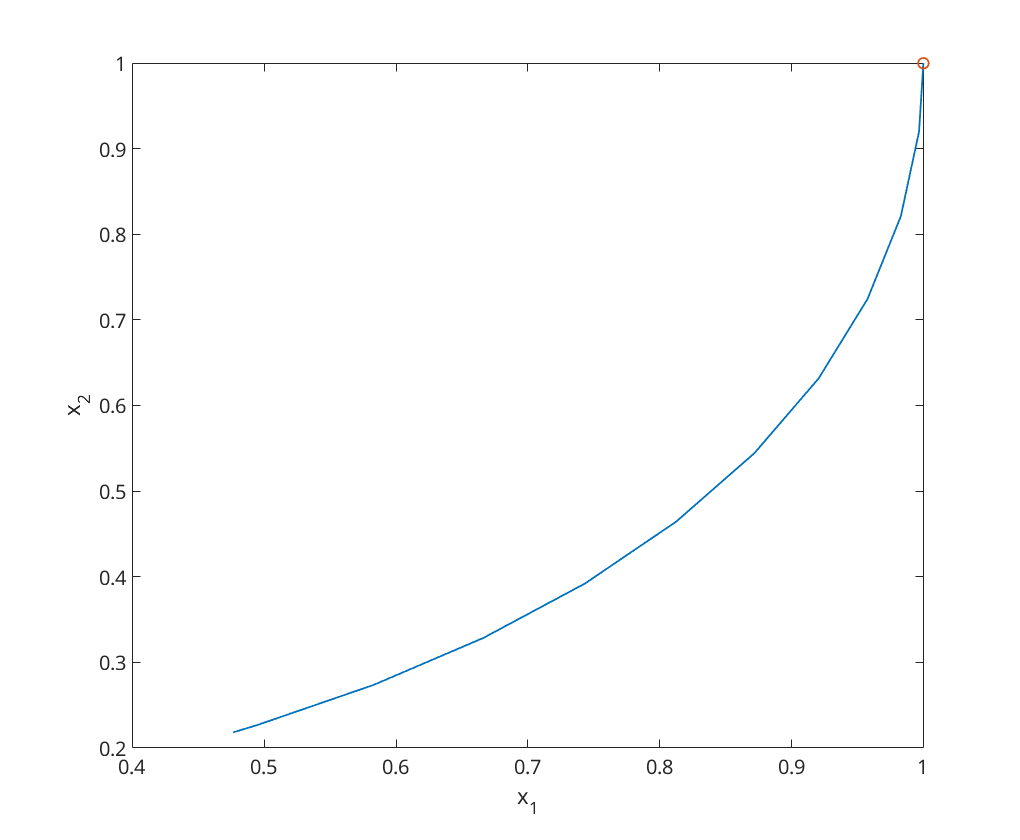
We start with 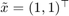 ,
, 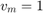 and
and 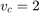 .
.
vm = 1; vc = 2; x0 = [1;1]; [~,x] = ode23(@(t,x) catmouse(t, x, vm, vc), [0, 1/vm], x0); figure; plot(x(:,1), x(:,2), x(1,1), x(1,2), 'o'); xlabel('x_1'); ylabel('x_2');
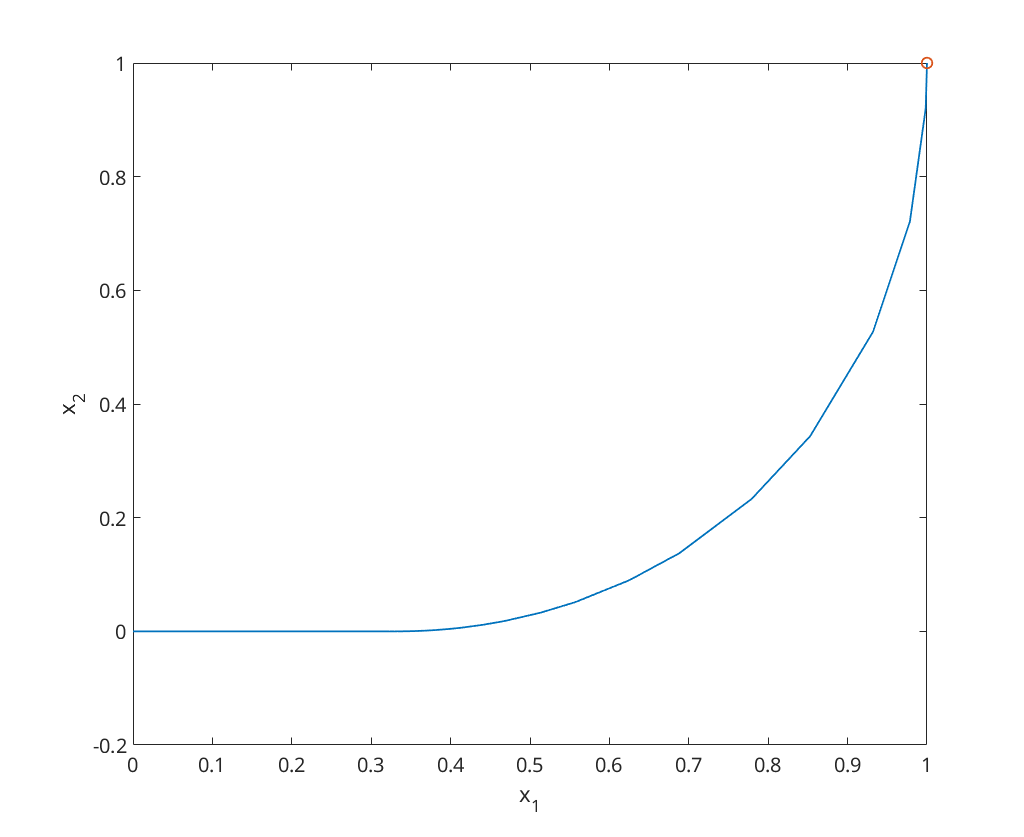
Now we consider 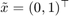 ,
, 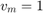 and
and 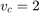 .
.
vm = 1; vc = 2; x0 = [0;1]; [~,x] = ode23(@(t,x) catmouse(t, x, vm, vc), [0, 1/vm], x0); figure; plot(x(:,1), x(:,2), x(1,1), x(1,2), 'o'); xlabel('x_1'); ylabel('x_2');
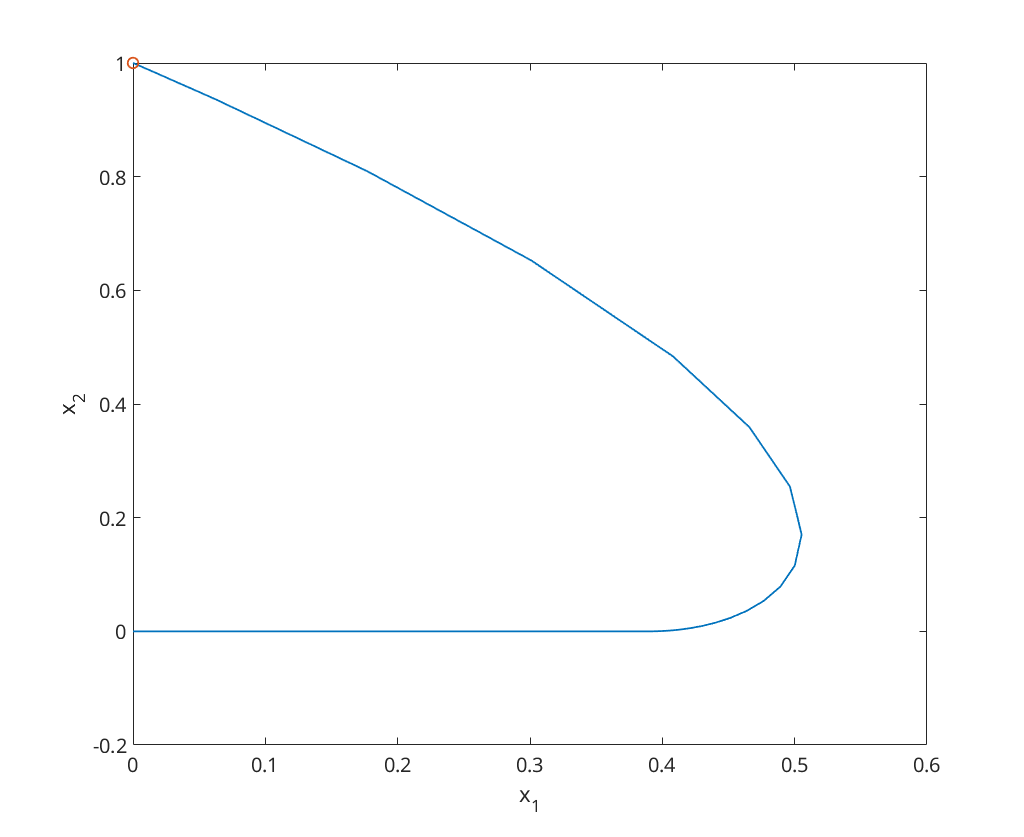
Finally we consider 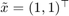 ,
, 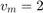 and
and 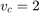 .
.
vm = 2; vc = 2; x0 = [1;1]; [~,x] = ode23(@(t,x) catmouse(t, x, vm, vc), [0, 1/vm], x0); figure; plot(x(:,1), x(:,2), x(1,1), x(1,2), 'o'); xlabel('x_1'); ylabel('x_2');
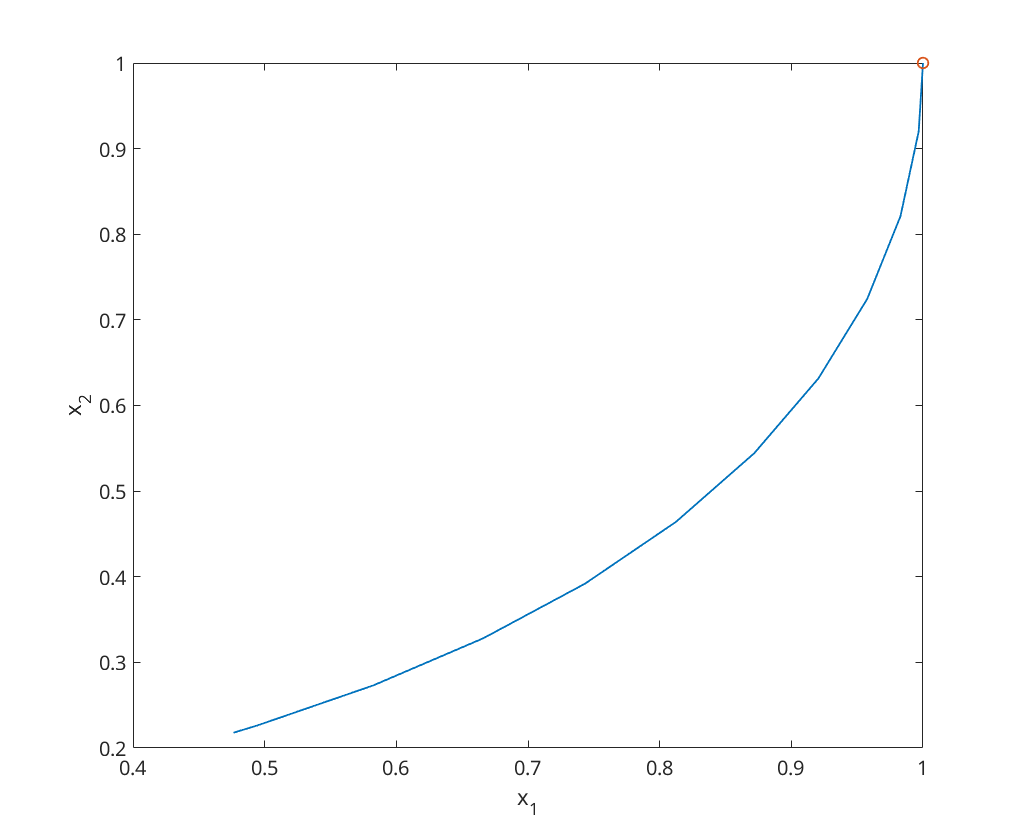
1(b)
With 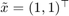 ,
, 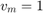 and
and 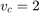 we zoom in around
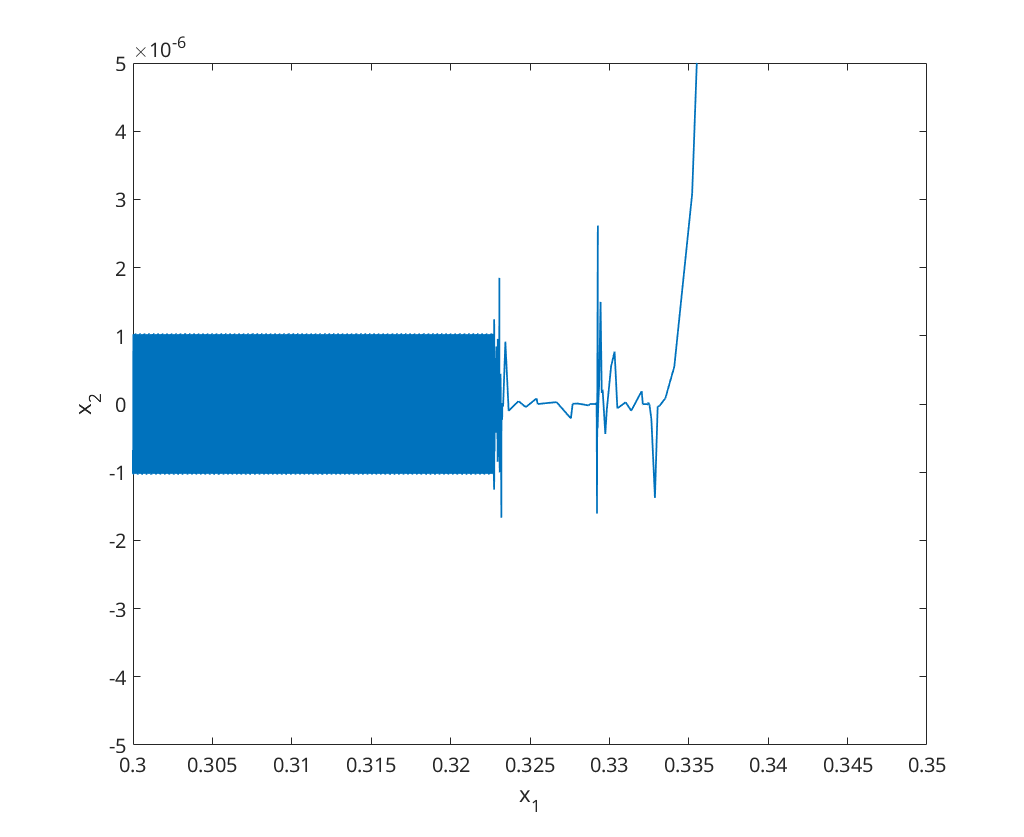
we zoom in around 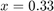 . We note here that we get small oscillations, which is caused because the cat has caught the mouse.
. We note here that we get small oscillations, which is caused because the cat has caught the mouse.
vm = 1; vc = 2; x0 = [1;1]; [~,x] = ode23(@(t,x) catmouse(t, x, vm, vc), [0, 1/vm], x0); figure; plot(x(:,1), x(:,2), x(1,1), x(1,2), 'o'); xlim([.3 .35]); ylim([-5e-6 5e-6]); xlabel('x_1'); ylabel('x_2');
1(c)
We now use events to detect when the distance between the mouse (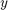 ) and the cat (
) and the cat ( ) is zero (
) is zero (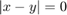 ); i.e., the cat has caught the mouse and use it to terminate the simulation
); i.e., the cat has caught the mouse and use it to terminate the simulation
vm = 1; vc = 2; x0 = [1;1]; options = odeset('Events',@(t, x) catmouseevents(t, x, vm)); [~,x,te,xe,ie] = ode23(@(t,x) catmouse(t, x, vm, vc), [0, 1/vm], x0, options); if ~isempty(ie) && (ie == 1) disp('Cat caught the mouse:'); fprintf(' At time: %f\n', te); fprintf(' Cat''s position: (%f, %f)\n', xe(1), xe(2)); else disp('The mouse reached its hole'); end figure; plot(x(:,1), x(:,2), x(1,1), x(1,2), 'o'); xlabel('x_1'); ylabel('x_2');
Cat caught the mouse: At time: 0.667549 Cat's position: (0.332461, 0.000000)
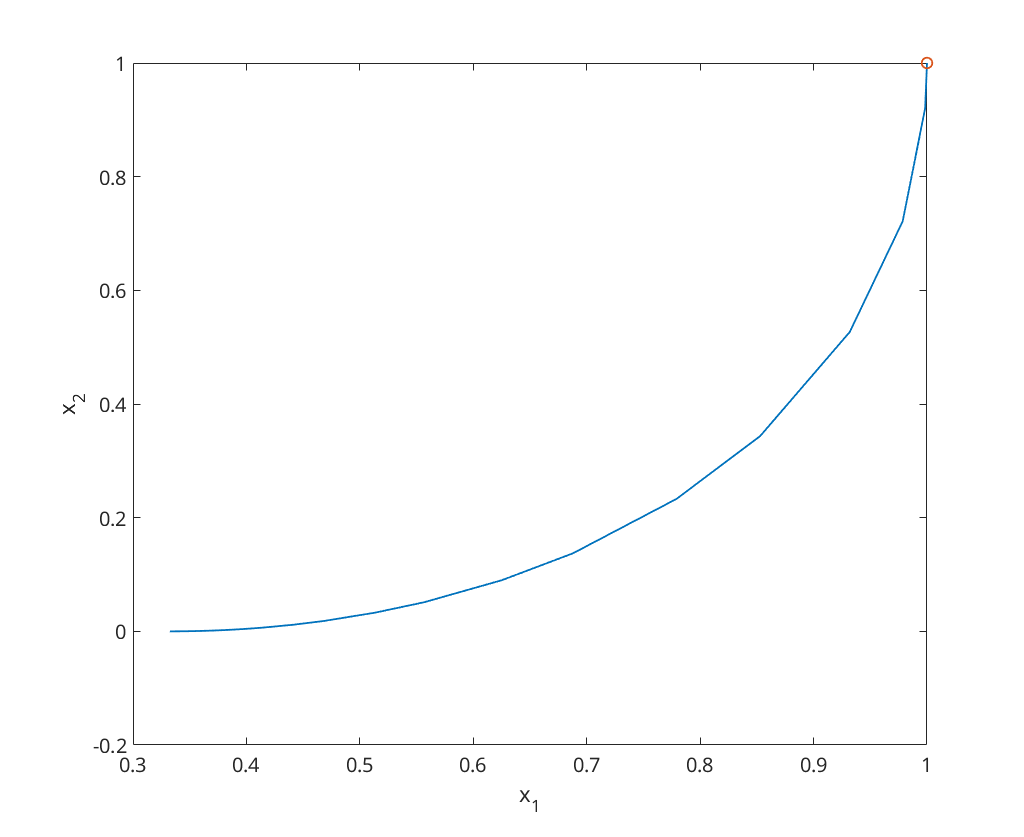
Now we test a case when the mouse doesn't catch the mouse: 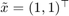 ,
, 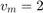 and
and 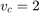
vm = 2; vc = 2; x0 = [1;1]; options = odeset('Events',@(t, x) catmouseevents(t, x, vm)); [~,x,te,xe,ie] = ode23(@(t,x) catmouse(t, x, vm, vc), [0, 1/vm], x0, options); if ~isempty(ie) && (ie == 1) disp('Cat caught the mouse:'); fprintf(' At time: %f\n', te); fprintf(' Cat''s position: (%f, %f)\n', xe(1), xe(2)); else disp('The mouse reached its hole'); end figure; plot(x(:,1), x(:,2), x(1,1), x(1,2), 'o'); xlabel('x_1'); ylabel('x_2');
The mouse reached its hole