Question 1(a) - Logistic equation

Comparison of Euler, Runge, and Runge-Kutta for 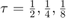$\tau=\frac12,\frac14,\frac18$ to ode23

Contents

Initial Setup

a=1;
b=1;
logistic = @(t,x)(a-b*x)*x;
x0 = 2;
t0 = 0;
T = 3;

Euler

figure;
[t,x]=ode23(logistic, [t0, T], x0);
plot(t,x,'-k','DisplayName','ode23');
hold on;

xlabel('time');
ylabel('x');
[t,x]=eul(logistic, t0, T, x0, 1/2); plot(t,x,'-ro','DisplayName','Euler (\tau=1/2)');
[t,x]=eul(logistic, t0, T, x0, 1/4); plot(t,x,'-bx','DisplayName','Euler (\tau=1/4)');
[t,x]=eul(logistic, t0, T, x0, 1/8); plot(t,x,'-m+','DisplayName','Euler (\tau=1/8)');
legend('Location','NorthEast');

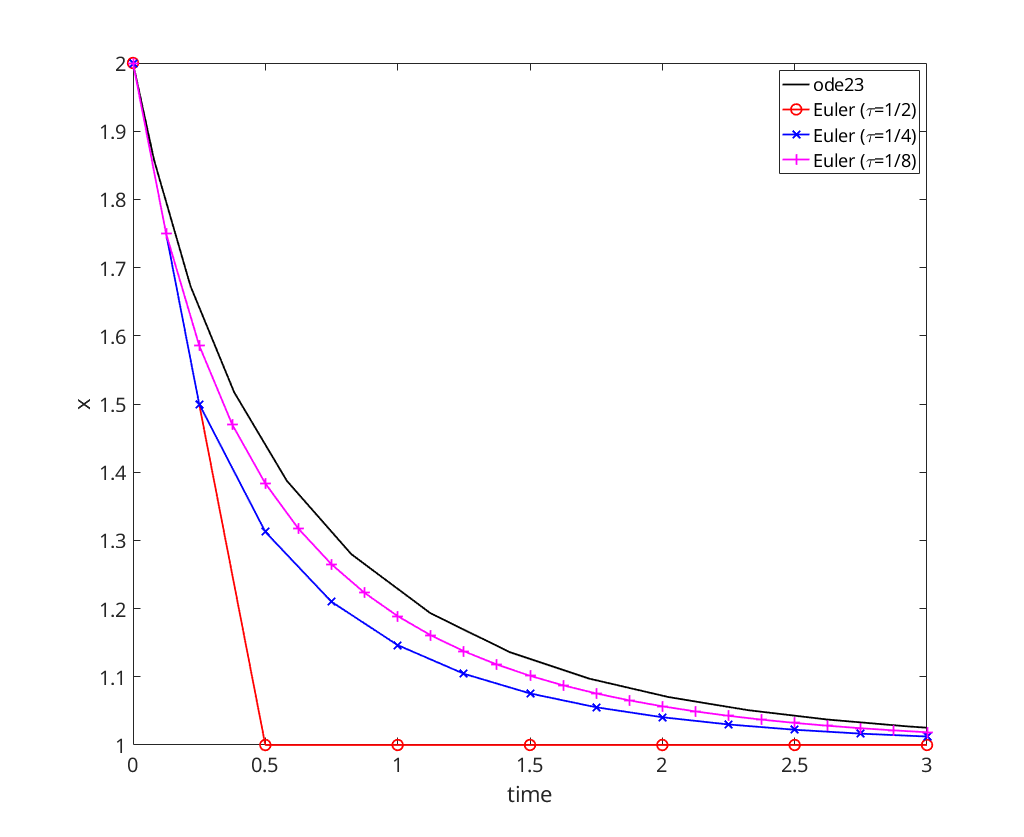
We note that Euler appears to (considerably) underestimate the solution, but tends to the solution as 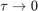$\tau \rightarrow 0$.

Runge

figure;
[t,x]=ode23(logistic, [t0, T], x0);
plot(t,x,'-k','DisplayName','ode23');
hold on;

xlabel('time');
ylabel('x');
[t,x]=runge(logistic, t0, T, x0, 1/2); plot(t,x,'-ro','DisplayName','Runge (\tau=1/2)');
[t,x]=runge(logistic, t0, T, x0, 1/4); plot(t,x,'-bx','DisplayName','Runge (\tau=1/4)');
[t,x]=runge(logistic, t0, T, x0, 1/8); plot(t,x,'-m+','DisplayName','Runge (\tau=1/8)');
legend('Location','NorthEast');

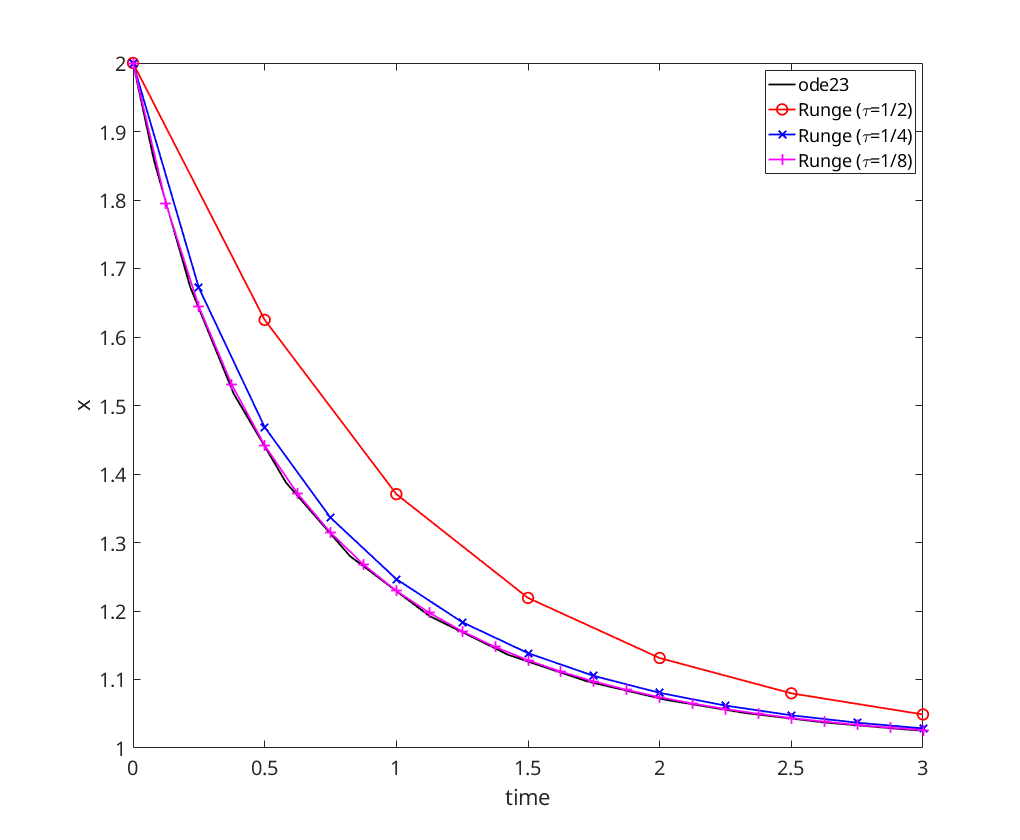
We note that Runge appears to overestimate the solution, but tends to the solution as $\tau \rightarrow 0$.

Runge-Kutta

figure;
[t,x]=ode23(logistic, [t0, T], x0);
plot(t,x,'-k','DisplayName','ode23');
hold on;

xlabel('time');
ylabel('x');
[t,x]=rk_classical(logistic, t0, T, x0, 1/2); plot(t,x,'-ro','DisplayName','Runge-Kutta (\tau=1/2)');
[t,x]=rk_classical(logistic, t0, T, x0, 1/4); plot(t,x,'-bx','DisplayName','Runge-Kutta (\tau=1/4)');
[t,x]=rk_classical(logistic, t0, T, x0, 1/8); plot(t,x,'-m+','DisplayName','Runge-Kutta (\tau=1/8)');
legend('Location','NorthEast');

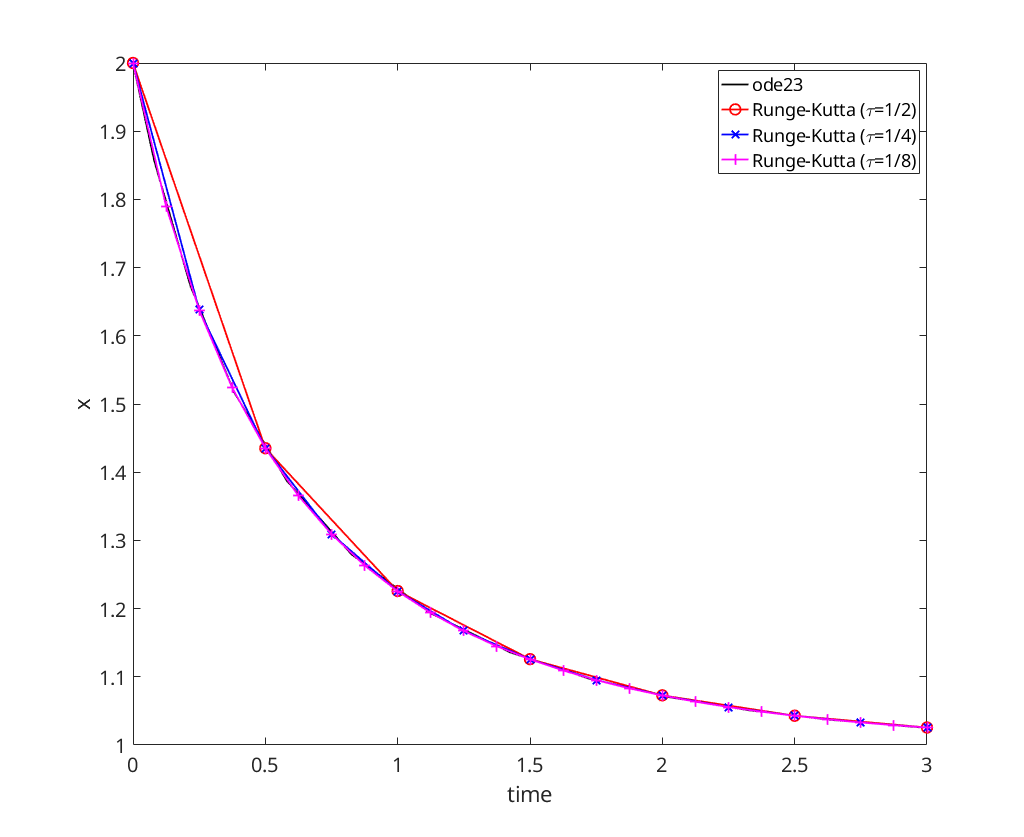
We note that Runge-Kutta seems to estimate the solution accurately (at the discrete points of evaluation) for all $\tau$.

Published with MATLAB® R2023a