Question 4 - Crank-Nicholson

Contents

Test Crank-Nicholson

function q4_solution

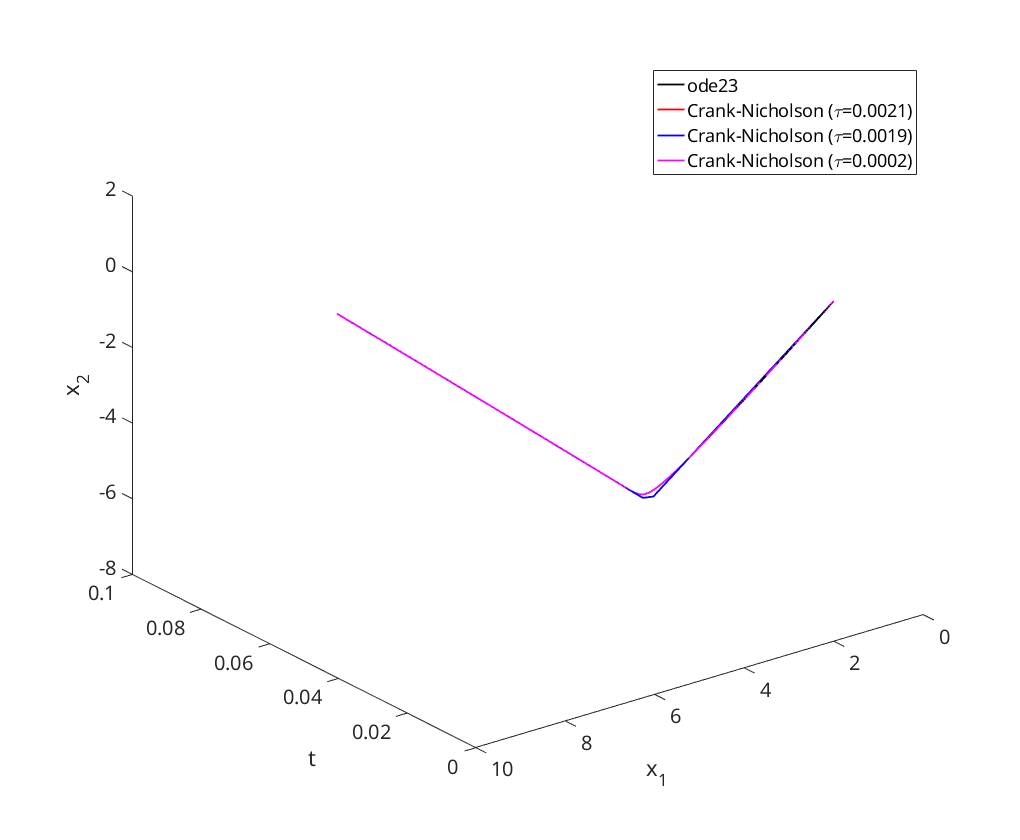
opt = odeset('RelTol',1e-5,'AbsTol',1e-6); % increase precision
t0 = 0;
T = 0.1;
x0 = [2; 1];

figure;
[t,x]=ode23(@linsystem, [t0, T], x0, opt);
plot3(t, x(:,1), x(:,2), 'k', 'DisplayName', 'ode23');
hold on;
xlabel('t');
ylabel('x_1');
zlabel('x_2');
view(-127.5, 30);
xlim([0, 0.1]);
ylim([0 10]);
zlim([-8 2]);
[te,xe] = crank_nicholson(@linsystem, t0, T, x0, 0.0021);
plot3(te, xe(:,1), xe(:,2), '-r', 'DisplayName', 'Crank-Nicholson (\tau=0.0021)');
te
xe
[te,xe] = crank_nicholson(@linsystem, t0, T, x0, 0.0019);
plot3(te, xe(:,1), xe(:,2), '-b', 'DisplayName', 'Crank-Nicholson (\tau=0.0019)');
[te,xe] = crank_nicholson(@linsystem, t0, T, x0, 0.0002);
plot3(te, xe(:,1), xe(:,2), '-m', 'DisplayName', 'Crank-Nicholson (\tau=0.0002)');
legend('Location','NorthEast');

te =

                   0
   0.002100000000000
   0.004200000000000
   0.006300000000000
   0.008400000000000
   0.010500000000000
   0.012600000000000
   0.014700000000000
   0.016800000000000
   0.018900000000000
   0.021000000000000
   0.023100000000000
   0.025200000000000
   0.027300000000000
   0.029400000000000
   0.031500000000000
   0.033600000000000
   0.035700000000000
   0.037800000000000
   0.039900000000000
   0.042000000000000
   0.044100000000000
   0.046200000000000
   0.048300000000000
   0.050400000000000
   0.052500000000000
   0.054600000000000
   0.056700000000000
   0.058800000000000
   0.060900000000000
   0.063000000000000
   0.065100000000000
   0.067200000000000
   0.069300000000000
   0.071400000000000
   0.073500000000000
   0.075600000000000
   0.077700000000000
   0.079800000000000
   0.081900000000000
   0.084000000000000
   0.086100000000000
   0.088200000000000
   0.090300000000000
   0.092400000000000
   0.094500000000000
   0.096600000000000
   0.098700000000000
   0.100800000000000


xe =

     2     1
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN
   NaN   NaN

For 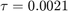$\tau=0.0021$ the solver does not converge

Crank-Nicholson function

function [t,x] = crank_nicholson(field, t0, T, x0, h)
%CRANK_NICHOLSON Implements the Crank-Nicholson one-step ODE solver
%
% Parameters:
%  field  -- Right hand side function of ODE system: x'=f(t,x)
%  t0     -- Initial time
%  T      -- End time (T > t0)
%  x0     -- Initial value
%  h      -- Size of time step (h <= T-t0)
%
% Outputs:
%  t  -- [t0; t-0+h, t0+2*h; ...; t0+i*h; ...]
%  x  -- Matrix containing numerical solution, with each row the value of x
%        at each time step

% Tolerance to use for solving the fixed point iteration
tol = 0.01;

n = ceil((T-t0)/h);
t = t0+h*(0:n).';
x = ones(n+1,length(x0));
x(1,:) = x0;

for i=1:n
    k1 = feval(field, t(i), x(i,:).');
    k2_old = k1; % k2_old = k2^{(0)}
    k2_new = feval(field, t(i)+h, x(i,:).'+h*(k1+k2_old)/2); % k2_new = k2^{(1)}
    while norm(k2_old-k2_new, 'inf') >= tol
        k2_old = k2_new; % k2^{(n)}
        k2_new = feval(field, t(i)+h, x(i,:).'+h*(k1+k2_old)/2); % k2^{(n+1)}
    end
    x(i+1,:) = x(i,:).' + h*(k1+k2_new)/2;
end
end

end

Published with MATLAB® R2023a