Question 2 (Modified ode12)

Contents

Test cases

Compare ode12 (Euler & Huen) to ode12_modified (Euler & Runge)

function q2_solution

[t,x] = ode12(@linsystem, 0, 0.1, [2 1]);
[t1,x1] = ode12_modified(@linsystem, 0, 0.1, [2 1]);

plot(t, x(:,1), '-ms', 'DisplayName', 'x_1 (ode12)');
hold on;
plot(t, x(:,2), '-ks', 'DisplayName', 'x_2 (ode12)');

plot(t1, x1(:,1), '-bx', 'DisplayName', 'x_1 (ode12\_modified)');
plot(t1, x1(:,2), '-rx', 'DisplayName', 'x_2 (ode12\_modified)');
legend('Location', 'east');
xlabel('t');

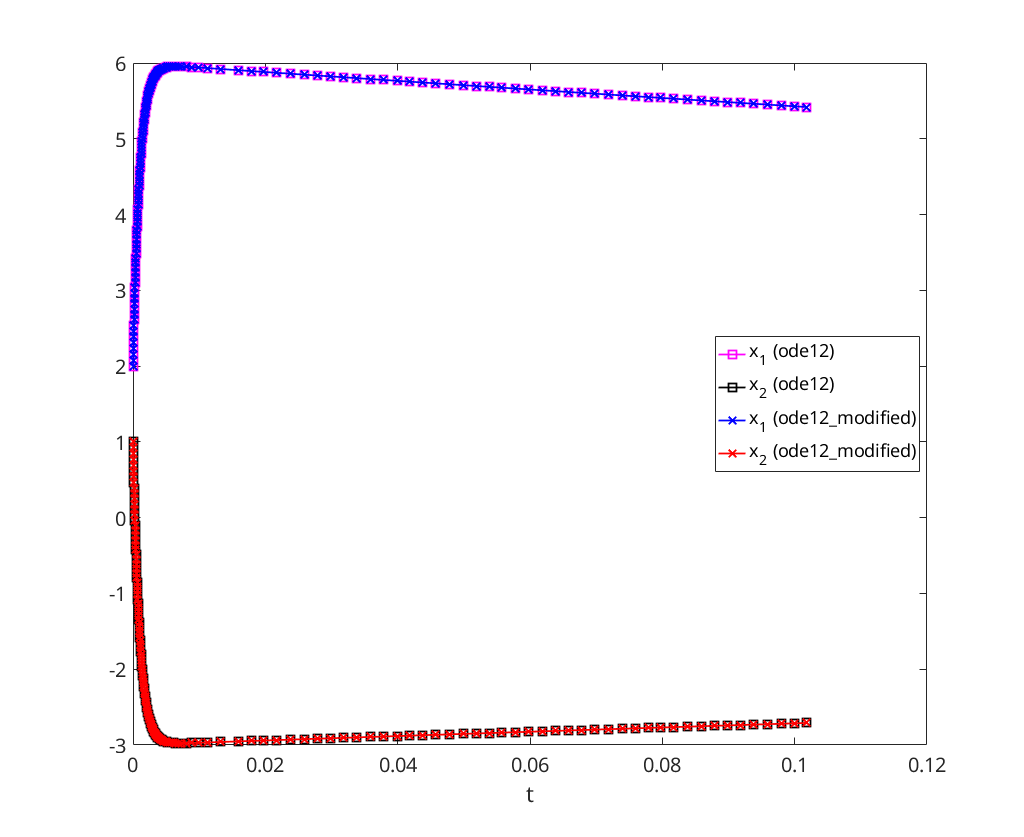
Modified ode12 - Euler (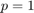$p=1$) and Runge ($p+1=2$)

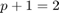function [t,x] = ode12_modified(field, t0, T, x0)

t = [t0];
x = zeros(1, length(x0));
x(1,:) = x0;
hmax = (T - t0)/16; % change from ode12_2
h = hmax/8;  % change from ode12_2
tol = 0.001;
power = 1/2; % = 1/(p+1)

while t(end) <= T
    k1 = feval(field, t(end), x(end,:).');
    k2 = feval(field, t(end)+h/2, x(end,:).'+h*k1/2);
    % Euler: x(i,:).' + h*k1;
    % Runge:  x(i,:).' + h*k2;
    % => Runge-Euler = h*(k2-k1);
    delta = norm(h*(k2-k1), 'inf');
    if delta <= tol
        % delta less than tolerance, so next timepoint and solution
        % computed by Runge
        t = [t;t(end)+h];
        x = [x; x(end,:)+h*k2.'];
    end
    if delta ~= 0.0
        h = min(hmax, 0.9*h*(tol/delta)^power);
    end
end

end

end

Published with MATLAB® R2023a