Q2 Solution

Contents

Logistic Method - Modified Adams-Bashfort 2-step

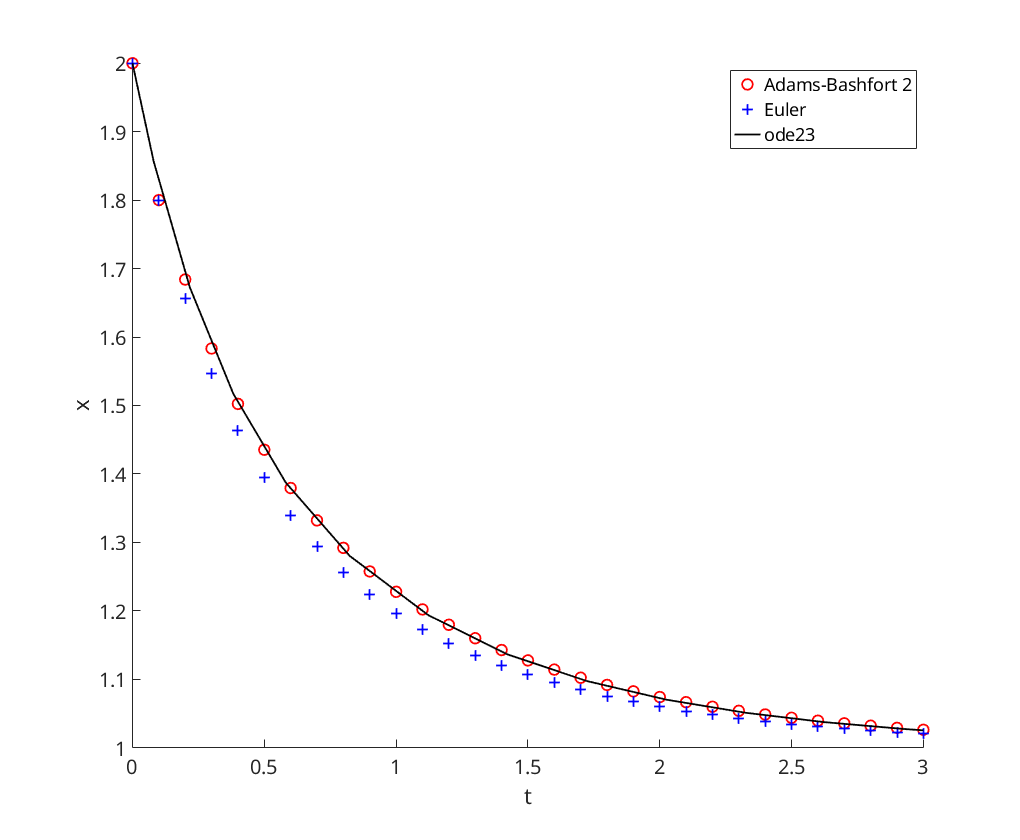
We solve the logistic problem

$x'=(1-x)*x, x(0)=2$

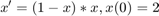
using Adams-Bashfort 2 (using Euler), Euler, and ode23

function q2_solution

figure;
axis([0 3 1 2]);
hold on;
xlabel('t');
ylabel('x');
[t,x]=ab2_modified(@logistic,0,3, 2, .1);
plot(t,x(:,1),'ro','DisplayName','Adams-Bashfort 2');

[t,x]=eul(@logistic,0,3, 2, .1);
plot(t,x(:,1),'b+','DisplayName','Euler');

[t,x]=ode23(@logistic,[0,3], 2);
plot(t,x(:,1),'k-','DisplayName','ode23');

legend('Location', 'NorthEast');

Linear Oscillator - Modified Adams-Bashfort 2-step

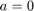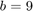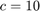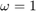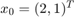We solve linear oscillator with $a = 0$, $b = 9$, $c = 10$, $\omega = 1$ and $x_0=(2,1)^T$ using Adams-Bashfort 2 (using Euler), Euler, and ode23.

figure
axis([0 10 -4 4]);
hold on;
xlabel('x_1');
ylabel('x_2');
[t,x]=ab2_modified(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'ro','DisplayName','Adams-Bashfort 2');

[t,x]=eul(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'b+','DisplayName','Euler');

% compare with  ode23
[t,x]=ode23(@oscillator,[0,10], [2;1]);
plot(t,x(:,1),'k-','DisplayName','ode23');

legend('Location', 'NorthEast');

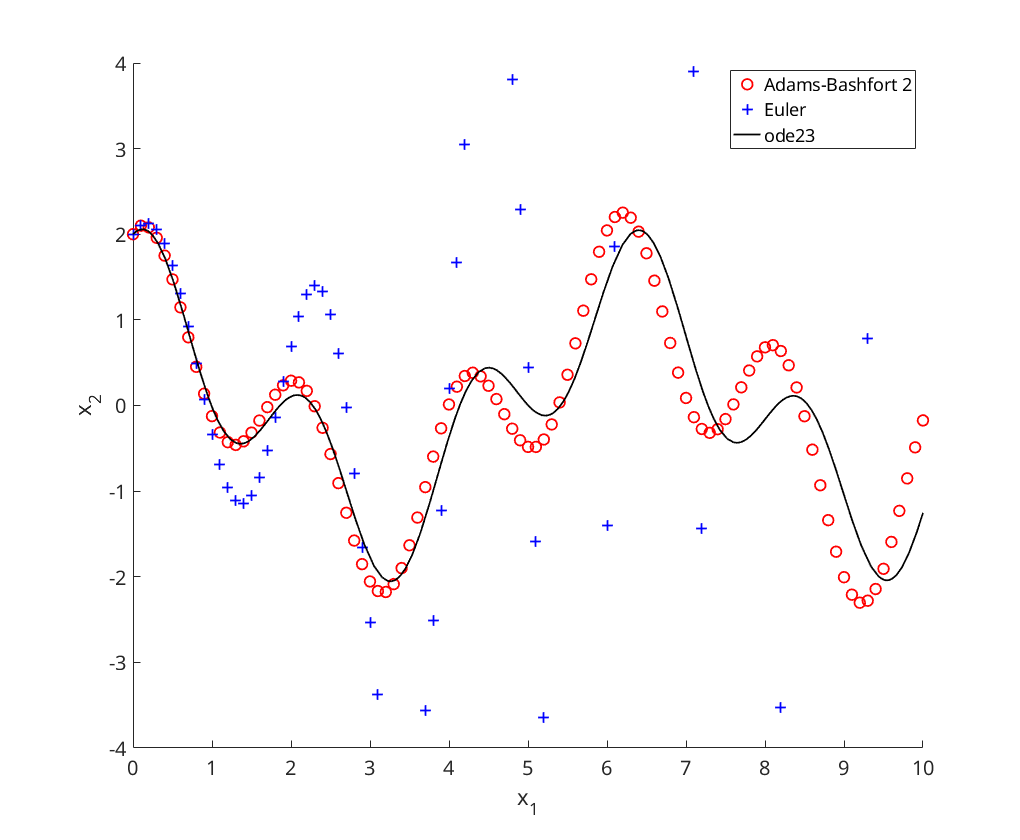
Linear Oscillator - Modified Adams-Bashfort 3-step

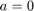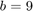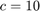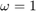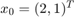We solve linear oscillator with $a = 0$, $b = 9$, $c = 10$, $\omega = 1$ and $x_0=(2,1)^T$ using Adams-Bashfort 2 (using Euler), Adams-Bashfort 3, and ode23.

figure
axis([0 10 -4 4]);
hold on;
xlabel('x_1');
ylabel('x_2');
[t,x]=ab2_modified(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'ro','DisplayName','Adams-Bashfort 2');

[t,x]=ab3_modified(@oscillator,0,10, [2;1], .1);
plot(t,x(:,1),'b+','DisplayName','Adams-Bashfort 3');

% compare with  ode23
[t,x]=ode23(@oscillator,[0,10], [2;1]);
plot(t,x(:,1),'k-','DisplayName','ode23');

legend('Location', 'NorthEast');

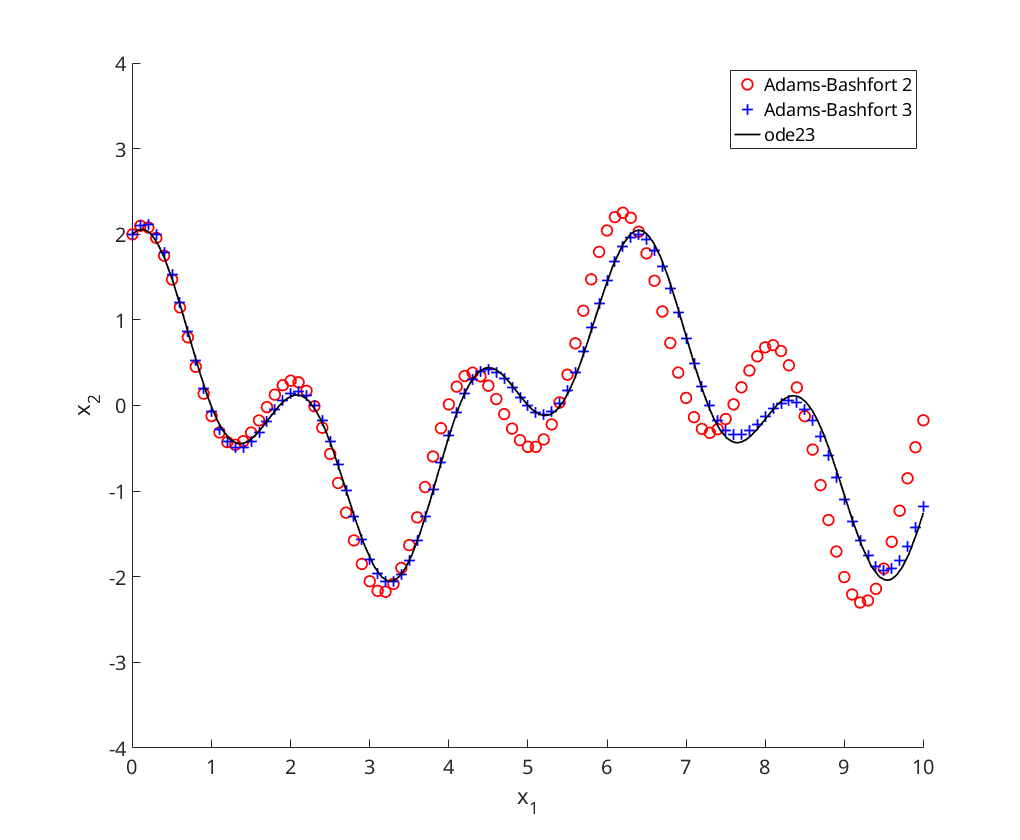
Convergence Analysis for Modified Adams-Bashfort

We perform convergence analysis for 2-step and 3-step Adams-Bashfort with Euler initialisation

fprintf('Adams-Bashfort 2-step: = ');
conv_analysis(@ab2_modified);
fprintf('Adams-Bashfort 3-step: = ');
conv_analysis(@ab3_modified);

Adams-Bashfort 2-step: = log_{10}E_N = -0.682247 + 2.092454 x log10(h)
Adams-Bashfort 3-step: = log_{10}E_N = -0.165385 + 2.194846 x log10(h)

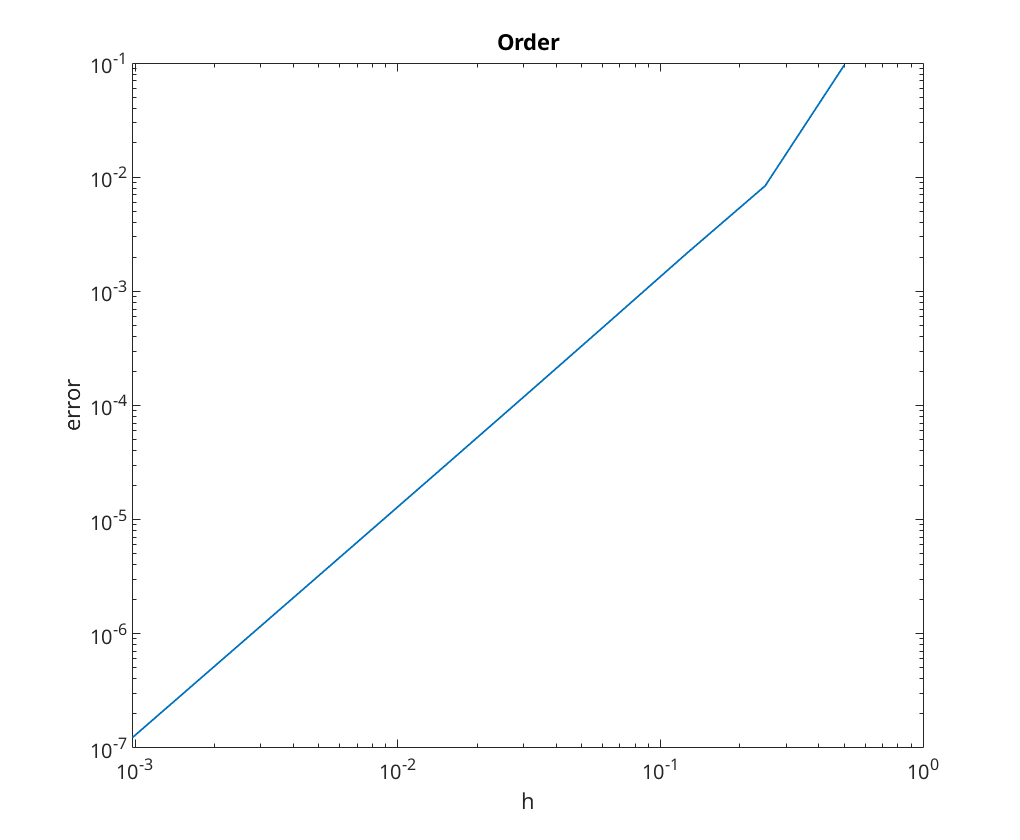
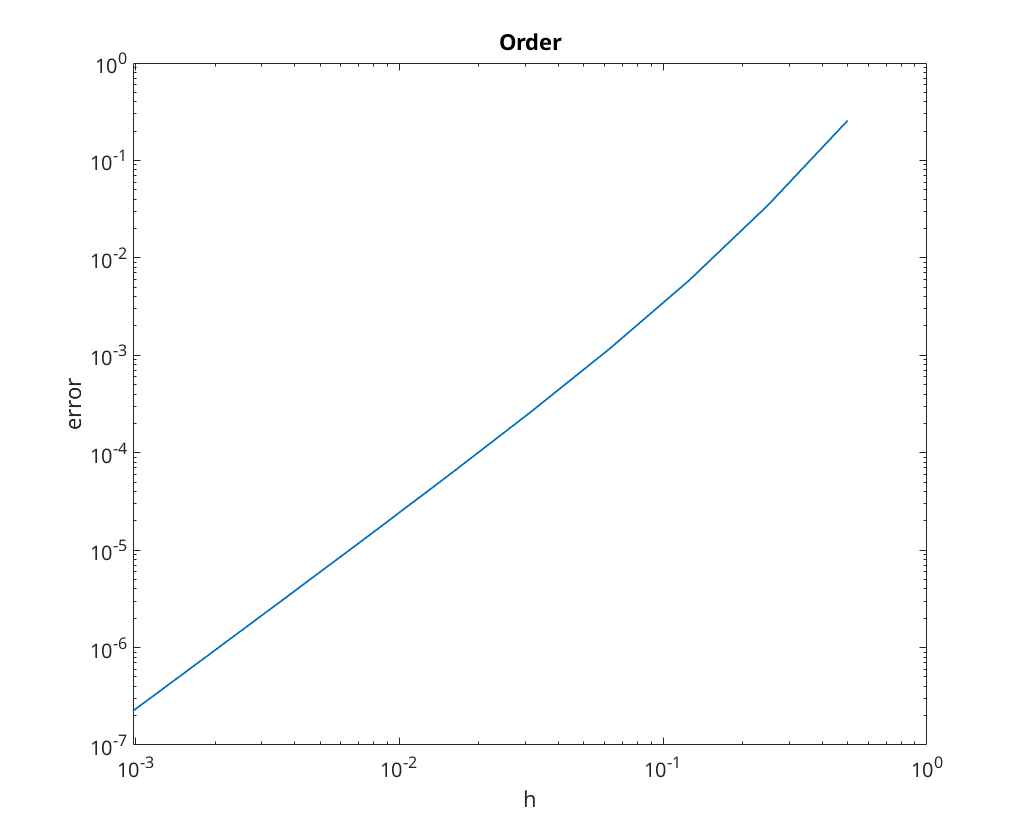
We note that for Adams-Bashfort 3-step we get a lower order of convergence than expected; caused by the fact that the initialisation is the limiting factor of the convergence.

Adams Bashfort 2 with Euler for initialisation

function [t,x] = ab2_modified(field, t0, T, x0, h)

m = 2;
n = ceil((T-t0)/h);

t = t0+h*(0:n).';
x = ones(n+1,length(x0));
[t(1:m), x(1:m,:)] = eul(field, t0, t0+(m-1)*h, x0, h);

f1 = feval(field, t(m-1), x(m-1,:).');
for i=m:n
    f0 = feval(field, t(i), x(i,:).');
    x(i+1,:) = x(i,:).' + h*(3*f0-f1)/2;
    f1 = f0;
end

end

Adams Bashfort 3 with Euler for initialisation

function [t,x] = ab3_modified(field, t0, T, x0, h)

m = 3;
n = ceil((T-t0)/h);

t = t0+h*(0:n).';
x = ones(n+1,length(x0));
[t(1:m), x(1:m,:)] = eul(field, t0, t0+(m-1)*h, x0, h);

f2 = feval(field, t(m-2), x(m-2,:).');
f1 = feval(field, t(m-1), x(m-1,:).');
for i=m:n
    f0 = feval(field, t(i), x(i,:).');
    x(i+1,:) = x(i,:).' + h*(23*f0-16*f1+5*f2)/12;
    f2 = f1;
    f1 = f0;
end

end

end

Published with MATLAB® R2023a