Question 1

We consider the linearised version of the pendulum with dynamical friction:

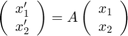
$\left(\begin{array}{c} x_1'\\ x_2'\end{array}\right) = A\left(\begin{array}{c} x_1 \\ x_2\end{array}\right)$

where

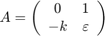
$A = \left(\begin{array}{cc} 0 & 1 \\ -k & \varepsilon \end{array}\right)$

with initial condition $x_0\in\bf{R}^2$ at time $t_0$ .

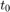A = [ 0 1; -1 -0.7 ];

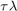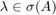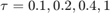We plot $\tau\lambda$ for all $\lambda\in\sigma(A)$ and $\tau=0.1,0.2,0.4,1$ against the domains of stability for the first, second, third and fourth order Runge-Kutta methods

figure;
hold on;
lambda=1;
plot(lambda*eig(A), 'ro', 'MarkerSize', 14);
lambda=0.4;
plot(lambda*eig(A), 'bo', 'MarkerSize', 14);
lambda=0.2;
plot(lambda*eig(A), 'mo', 'MarkerSize', 14);
lambda=0.1;
plot(lambda*eig(A), 'go', 'MarkerSize', 14);

rk_stab(1, 'r.');
rk_stab(2, 'b.');
rk_stab(3, 'm.');
rk_stab(4, 'g.');
xlim([-4 4]);
ylim([-4 4]);
axis('square');
xlabel('Re');
ylabel('Im');
legend('1\lambda','0.4\lambda','0.2\lambda','0.1\lambda', ...
    'First Order RK', 'Second Order RK', 'Third Order RK', 'Fourth Order RK');

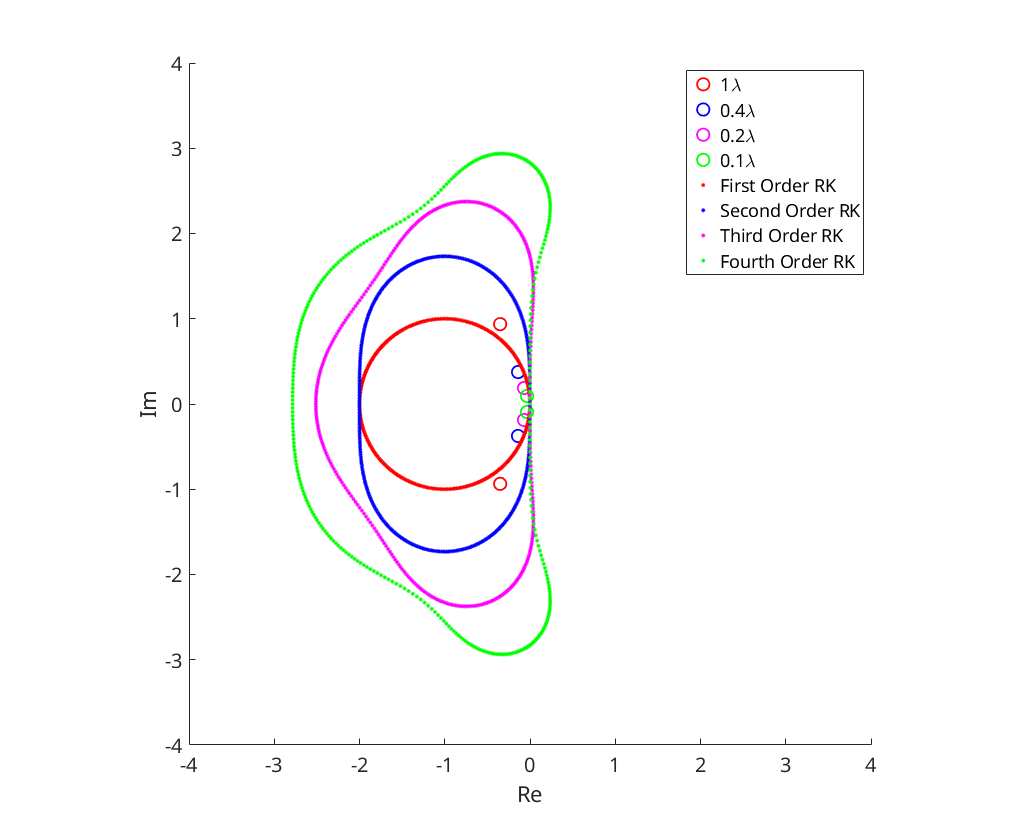
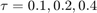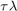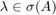We notice that all four Runge-Kutta methods are stable for $\tau=0.1,0.2,0.4$ as $\tau\lambda$ , for all $\lambda\in\sigma(A)$ , are inside the domains of stability for every method.

For 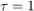$\tau=1$ we note that 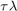$\tau\lambda$ , for all 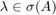$\lambda\in\sigma(A)$ , is outside the domain of stability for the first order Runge-Kutta indicating it is unstable for this value of $\tau$ .