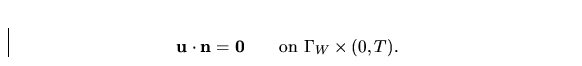Next: Initial Conditions
Up: Formulation of the Problem
Previous: Conservation Form of Equations
We will consider the so-called inflow-outflow problem. The problem of a fluid
moving through a channel or the problem of a flow past an air profile
belong to this class.
We distinguish the inlet part of the boundary 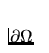
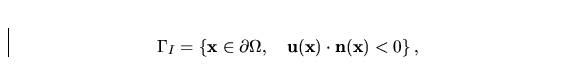
through which the fluid enters to the domain 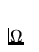 , the outlet part
, the outlet part
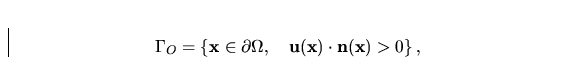
through which the fluid leaves the domain  and the rest of
the boundary
and the rest of
the boundary  , called the solid impermeable wall,
denoted by
, called the solid impermeable wall,
denoted by  . (
. (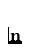 is the unit outer normal to
is the unit outer normal to
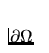 ).
).
(i) Viscous case, 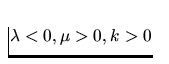
In this case, the system (15) is of the hyperbolic-parabolic type.
The first
equation is hyperbolic and the others are parabolic. Due to the viscosity
of the fluid the particles adhere to the solid wall and one has to prescribe
the no-slip boundary condition
| 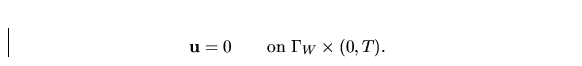 |
(17) |
Some theoretical results and also our numerical experiments lead us to the
use of
the following boundary conditions:
(ii) Inviscid case, 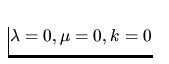
The system of Euler equations (17) is hyperbolic. In this case the
number of boundary conditions on 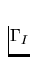 and
and 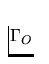 is
different if the flow is subsonic (
is
different if the flow is subsonic (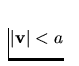 ) or
supersonic (
) or
supersonic (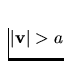 ), where a is the local sound speed given
by
), where a is the local sound speed given
by

More precisely we will speak about this in the following section.
On 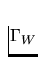 we prescribe a zero normal component of the velocity because
the wall is impermeable, i.e.
we prescribe a zero normal component of the velocity because
the wall is impermeable, i.e.
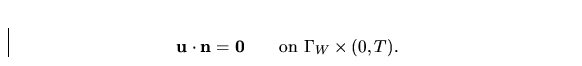



Next: Initial Conditions
Up: Formulation of the Problem
Previous: Conservation Form of Equations
Vit Dolejsi
12/17/1998
![]()
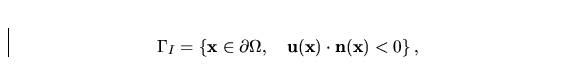
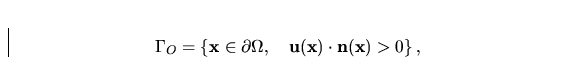
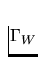 . (
. (
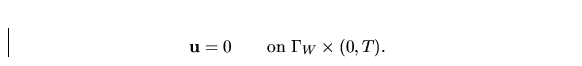
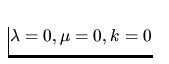
![]() and
and ![]() is
different if the flow is subsonic (
is
different if the flow is subsonic (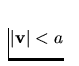 ) or
supersonic (
) or
supersonic (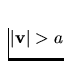 ), where a is the local sound speed given
by
), where a is the local sound speed given
by

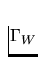 we prescribe a zero normal component of the velocity because
the wall is impermeable, i.e.
we prescribe a zero normal component of the velocity because
the wall is impermeable, i.e.