


Next: Shorův faktorizační algoritmus
Up: Kvantové algoritmy
Previous: Klasická kryptografie
Obsah
Kryptosystém RSA (který v roce 1978 vymysleli Ronald Rivest, Adi Shamir a
Leonard Adlemann) je založen na problému faktorizace velkých čísel.
Podívejme se na to, jak tento systém řeší přenos zprávy mezi dvěma místy.
Nejprve musí přijímající strana (v tomto případě Bob)
vygenerovat pár klíčů, z nichž jeden je tzv. veřejný klíč, který
je k dispozici všem a Bob jej sdělí veřejným kanálem Alici. Alice tímto klíčem
zprávu zašifruje (tuto část komunikace může provést kdokoliv).
V této chvíli přichází na řadu druhý klíč - privátní, který Bob nikomu
nesdělil. Alice pošle zašifrovanou zprávu Bobovi, který si ji svým
privátním klíčem dešifruje. Aby to však bylo možné, je nutné, aby byly
oba klíčem určitým způsobem propojeny. Pojďme se teď na toto spojení podívat
podrobněji. Aby byl RSA systém bezpečný, musí být těžké na základě znalosti
veřejného klíče a zašifrované zprávy od Alice zjistit otevřenou hodnotu zprávy
(to také znamená, že ze znalosti těchto hodnot musí být těžké zjistit
klíč privátní). Toho RSA dociluje tím, že spoléhá na neschůdnost faktorizace
velkých celých čísel. Řekněme, že Bob chce komunikovat s Alicí. Konkrétní
postup při komunikaci se skládá jednak z části generování klíče
(první tři body) a části komunikační:
- Bob si nejdříve vybere dvě dostatečně velká prvočísla
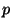 a
a 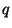 , která
vynásobí a získá číslo
, která
vynásobí a získá číslo 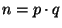 .
.
- Poté začne počítat dvě celá čísla
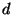 a
a 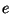 tak, že za
tak, že za 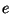 si zvolí
náhodné číslo, které je nesoudělné s číslem
si zvolí
náhodné číslo, které je nesoudělné s číslem
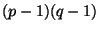 . Dále musí
vypočítat
. Dále musí
vypočítat 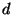 z výrazu
z výrazu
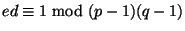 .
.
- Následuje zaslání veřejného klíče Alici jako páru čísel {
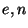 }.
}.
- Vytvoření zprávy
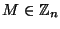 .
.
- Nyní Alice zašifruje zprávu pomocí veřejného klíče jako
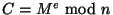 .
.
- Tu pak zašle Bobovi, který na základě znalosti svého utajeného
privátního klíče dešifruje jako
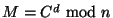 a potom
převede zpět do textové podoby.
a potom
převede zpět do textové podoby.
Ukažme si celou proceduru na vysvětlujícím příkladu:
Bob si například zvolí 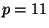 a
a 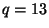 , dále je
, dále je
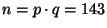 .
Jestliže si za
.
Jestliže si za 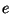 zvolí například číslo 7 (nesoudělné s
zvolí například číslo 7 (nesoudělné s
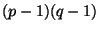 a zároveň menší než toto číslo), pak z rovnice
a zároveň menší než toto číslo), pak z rovnice
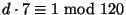 je
je 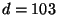 .
Tím má Bob k zaslání připraven
veřejný klíč (7, 143) a k uschování privátní klíč (103, 143).
Veřejným klíčem Alice zašifruje třeba písmeno x, které je v našem číselném
kódu rovno řekněme 16. Takže je pak
.
Tím má Bob k zaslání připraven
veřejný klíč (7, 143) a k uschování privátní klíč (103, 143).
Veřejným klíčem Alice zašifruje třeba písmeno x, které je v našem číselném
kódu rovno řekněme 16. Takže je pak
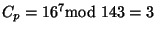 .
To si Bob dešifruje jako
.
To si Bob dešifruje jako
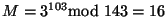 , tj. kód
písmene x. Pro velká čísla nepřipadá prolomení hrubou silou v úvahu,
protože k tomu by bylo potřeba zjistit
, tj. kód
písmene x. Pro velká čísla nepřipadá prolomení hrubou silou v úvahu,
protože k tomu by bylo potřeba zjistit 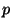 a
a 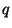 . Pak by byl již výpočet
. Pak by byl již výpočet 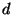 jednoduchý. Jako bezpečné se dnes obvykle uvažuje použití
jednoduchý. Jako bezpečné se dnes obvykle uvažuje použití 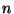 v délce 1024
bitů, sestavené ze dvou prvočísel přibližně poloviční délky.
v délce 1024
bitů, sestavené ze dvou prvočísel přibližně poloviční délky.



Next: Shorův faktorizační algoritmus
Up: Kvantové algoritmy
Previous: Klasická kryptografie
Obsah
Bashar
2001-01-23