



Next: Universal dendrites
Up: Dendrites
Previous: The locally connected fan
The next two
examples are defined in [Arévalo et al. 2001, p. 3]. Let
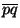 stand for the straight line segment from
stand for the straight line segment from
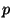 to
to 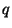 in the plane. In the plane, let
in the plane. In the plane, let
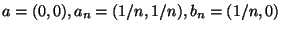 for each
for each
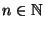 , and
, and
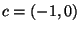 . Define
. Define
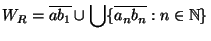
and
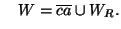
The dendrites 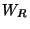 and
and 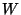 are called the
comb
are called the
comb 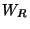 and the
comb
and the
comb 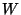 , or (generally)
locally connected combs
.
, or (generally)
locally connected combs
.
See Figures A-B.
Figure 1.3.4:
( A ) comb 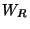
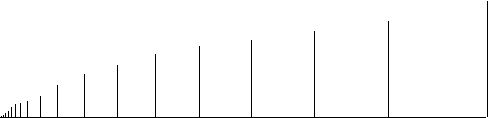 |
Figure 1.3.4:
( B ) comb 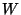
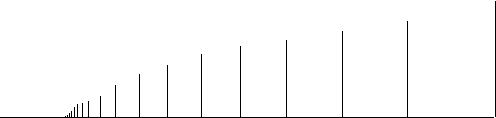 |
The dendrites 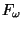 ,
, 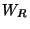 and
and 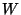 are exploited in the
following characterizations.
are exploited in the
following characterizations.
- A dendrite is a tree if and only if it contains neither a copy of
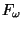 nor of
nor of 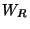 , [Arévalo et al. 2001, Theorem 3.1, p. 3].
, [Arévalo et al. 2001, Theorem 3.1, p. 3].
- A dendrite has the set of all
its end points closed if
and only if it contains neither a copy of
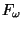 nor of
nor of 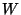 ,
[Arévalo et al. 2001, Corollary 5.4, p. 11].
,
[Arévalo et al. 2001, Corollary 5.4, p. 11].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.




Next: Universal dendrites
Up: Dendrites
Previous: The locally connected fan
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() and
and ![]() are called the
comb
are called the
comb ![]() and the
comb
and the
comb ![]() , or (generally)
locally connected combs
.
, or (generally)
locally connected combs
.
![]() ,
, ![]() and
and ![]() are exploited in the
following characterizations.
are exploited in the
following characterizations.