




Next: LOCALLY CONNECTED CONTINUA
Up: Examples in Continuum Theory
Previous: Contents
All spaces considered here are assumed to be metric (if
otherwise is not explicitly said) and all mappings are
assumed to be continuous. Concepts and notions undefined in
the text are used according to their meaning known from the
literature. To aviod any doubt or misunderstanding, the
reader can find the needed definition or explanation in
Appendix A, where the items are alphabetically ordered.
The following notation will be used. The symbol
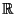 stands for the space of real numbers, equipped with the
natural topology. Thus
stands for the space of real numbers, equipped with the
natural topology. Thus
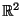 denotes the plane
(usually supplied with a Cartesian coordinate system);
equivalently, the plane can be denoted by
denotes the plane
(usually supplied with a Cartesian coordinate system);
equivalently, the plane can be denoted by
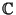 when
considered as the set of all complex numbers. The closed
unit interval
when
considered as the set of all complex numbers. The closed
unit interval ![[0,1]$](img35.gif) of reals is denoted by
of reals is denoted by
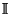 ,
and
,
and
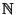 means the set of all positive integers.
means the set of all positive integers.





Next: LOCALLY CONNECTED CONTINUA
Up: Examples in Continuum Theory
Previous: Contents
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() stands for the space of real numbers, equipped with the
natural topology. Thus
stands for the space of real numbers, equipped with the
natural topology. Thus
![]() denotes the plane
(usually supplied with a Cartesian coordinate system);
equivalently, the plane can be denoted by
denotes the plane
(usually supplied with a Cartesian coordinate system);
equivalently, the plane can be denoted by
![]() when
considered as the set of all complex numbers. The closed
unit interval
when
considered as the set of all complex numbers. The closed
unit interval ![]() of reals is denoted by
of reals is denoted by
![]() ,
and
,
and
![]() means the set of all positive integers.
means the set of all positive integers.