




Next: Dendrites of de Groot-Wille
Up: Dendrites
Previous: Chaotic and rigid dendrites
Recall that a space is said to be
incompressible if it is
homeomorphic to no proper subspace of itself. The circle
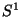 is an example of such a space. In 1925 Zarankiewicz
[Zarankiewicz 1925] asked whether there exists an
incompressible dendrite. The question has been answered in
the positive in 1932 by E. W. Miller [Miller 1932]. The
reader is referred to the original Miller's paper for the
(rather long) construction of the example. The main idea of
the proof is based on the following implication,
[Miller 1932, Theorem, p. 831].
is an example of such a space. In 1925 Zarankiewicz
[Zarankiewicz 1925] asked whether there exists an
incompressible dendrite. The question has been answered in
the positive in 1932 by E. W. Miller [Miller 1932]. The
reader is referred to the original Miller's paper for the
(rather long) construction of the example. The main idea of
the proof is based on the following implication,
[Miller 1932, Theorem, p. 831].
If a dendrite  contains a subset
contains a subset 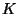 such that
such that
- A.
- each point of
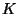 is fixed with respect to any homeomorphism of
is fixed with respect to any homeomorphism of
 onto a subcontinuum of
onto a subcontinuum of  ;
;
- B.
- each point of
 which is not an end point of
which is not an end point of  lies in an arc
contained in
lies in an arc
contained in  and having its end points in
and having its end points in 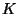 ,
,
then  is incompressible.
is incompressible.
The
Miller dendrite 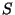 has the following properties, [Miller 1932].
has the following properties, [Miller 1932].
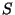 contains a subset
contains a subset 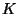 having properties A and B above, so it is
incompressible.
having properties A and B above, so it is
incompressible.
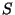 is not chaotic.
is not chaotic.
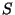 contains open arcs as open subsets, hence it is not rigid.
contains open arcs as open subsets, hence it is not rigid.
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.





Next: Dendrites of de Groot-Wille
Up: Dendrites
Previous: Chaotic and rigid dendrites
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() is an example of such a space. In 1925 Zarankiewicz
[Zarankiewicz 1925] asked whether there exists an
incompressible dendrite. The question has been answered in
the positive in 1932 by E. W. Miller [Miller 1932]. The
reader is referred to the original Miller's paper for the
(rather long) construction of the example. The main idea of
the proof is based on the following implication,
[Miller 1932, Theorem, p. 831].
is an example of such a space. In 1925 Zarankiewicz
[Zarankiewicz 1925] asked whether there exists an
incompressible dendrite. The question has been answered in
the positive in 1932 by E. W. Miller [Miller 1932]. The
reader is referred to the original Miller's paper for the
(rather long) construction of the example. The main idea of
the proof is based on the following implication,
[Miller 1932, Theorem, p. 831].
![]() contains a subset
contains a subset ![]() such that
such that
![]() has the following properties, [Miller 1932].
has the following properties, [Miller 1932].