




Next: indecomposable
Up: Definitions
Previous: HU-terminal
Given a continuum  with a metric
with a metric 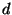 , we let
, we let 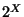 to denote the
hyperspace of all nonempty closed subsets of
to denote the
hyperspace of all nonempty closed subsets of  equipped with the
Hausdorff metric
equipped with the
Hausdorff metric 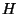 defined by
(see e.g. [Nadler 1978, (0.1), p. 1 and (0.12), p. 10]).
If
defined by
(see e.g. [Nadler 1978, (0.1), p. 1 and (0.12), p. 10]).
If 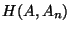 tends
to zero as
tends
to zero as 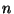 tends to infinity, we put
tends to infinity, we put
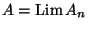 . Further, we denote
by
. Further, we denote
by 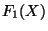 the hyperspace of singletons of
the hyperspace of singletons of  , and by
, and by 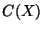 the hyperspace of all
subcontinua of
the hyperspace of all
subcontinua of  , i.e., of all connected elements of
, i.e., of all connected elements of 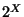 . Since
. Since  is
homeomorphic to
is
homeomorphic to 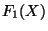 , there is a natural embedding of
, there is a natural embedding of  into
into 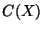 ,
and so we can write
,
and so we can write
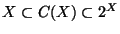 . Thus one can consider a
retraction from either
. Thus one can consider a
retraction from either 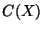 or
or 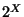 onto
onto  .
.





Next: indecomposable
Up: Definitions
Previous: HU-terminal
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30