



Next: Modifications of the Gehman
Up: Dendrites
Previous: Dendrites with the closed
One of the classical examples of dendrites with its set of
end points closed is the
Gehman dendrite
.
It can be described as a dendrite 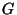 having the
set
having the
set 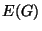 homeomorphic to the Cantor ternary set
homeomorphic to the Cantor ternary set 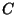 in
in
![[0,1]$](img35.gif) such that all ramification points of
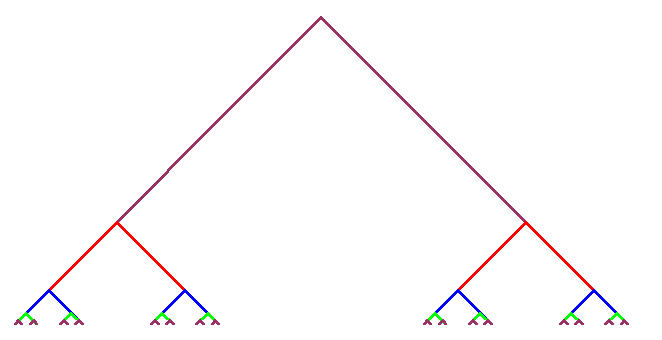
such that all ramification points of 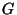 are of
order 3 (see [Gehman 1925, the example on p. 42]; see
also [Nikiel 1983, p. 422-423] for a geometrical
description; compare [Nikiel 1989, p. 82] and
[Nadler 1992, Example 10.39, p. 186]).
See Figure A.
are of
order 3 (see [Gehman 1925, the example on p. 42]; see
also [Nikiel 1983, p. 422-423] for a geometrical
description; compare [Nikiel 1989, p. 82] and
[Nadler 1992, Example 10.39, p. 186]).
See Figure A.
Figure 1.3.18:
( A ) Gehman dendrite
 |
The Gehman dendrite has the following properties.
- The set
 of all ramification points of
of all ramification points of  is discrete.
is discrete.
-
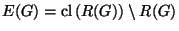 .
.
- Each dendrite with an uncountable set of its end points contains
a homeomorphic copy of the Gehman dendrite, [Arévalo et al. 2001, Proposition 6.8, p.
16].
- If a continuum contains the Gehman dendrite, then it does not
have the periodic-recurrent
property, [Charatonik 1998, Theorem 3.3, p. 136].
- A dendrite
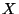 contains the Gehman dendrite if and only if
contains the Gehman dendrite if and only if 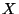 does not have the periodic-recurrent property,
[Illanes 1998, Theorem 2, p. 222].
does not have the periodic-recurrent property,
[Illanes 1998, Theorem 2, p. 222].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.




Next: Modifications of the Gehman
Up: Dendrites
Previous: Dendrites with the closed
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() having the
set
having the
set ![]() homeomorphic to the Cantor ternary set
homeomorphic to the Cantor ternary set ![]() in
in
![]() such that all ramification points of
such that all ramification points of ![]() are of
order 3 (see [Gehman 1925, the example on p. 42]; see
also [Nikiel 1983, p. 422-423] for a geometrical
description; compare [Nikiel 1989, p. 82] and
[Nadler 1992, Example 10.39, p. 186]).
See Figure A.
are of
order 3 (see [Gehman 1925, the example on p. 42]; see
also [Nikiel 1983, p. 422-423] for a geometrical
description; compare [Nikiel 1989, p. 82] and
[Nadler 1992, Example 10.39, p. 186]).
See Figure A.