




Next: semi-locally connected
Up: Definitions
Previous: semi-continuum
Let a continuum  , a compact space
, a compact space 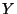 and a function
and a function
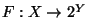 be given. Put
The function
be given. Put
The function 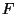 is said to be lower (upper) semi-continuous
provided that
is said to be lower (upper) semi-continuous
provided that 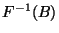 is open (closed) for each open (closed) subset
is open (closed) for each open (closed) subset
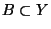 . It is said to be continuous provided that it is both
lower
and upper semi-continuous. This notion of continuity agrees with the one for
mappings between metric spaces.
. It is said to be continuous provided that it is both
lower
and upper semi-continuous. This notion of continuity agrees with the one for
mappings between metric spaces.





Next: semi-locally connected
Up: Definitions
Previous: semi-continuum
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30