Preliminary properties

The following properties of dendrites are known (see e.g. [Nadler 1992, Chapter 10, p. 165], [Kuratowski 1968, §51, VI, p. 300] or [Whyburn 1942, p. 88]; compare also [Charatonik et al. 1998, Theorems 1.3 and 1.5, p. 233]).

1. Every subcontinuum of a dendrite is a dendrite (thus each dendrite is hereditarily locally connected).
2. Every connected subset of a dendrite is arcwise connected.
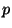3. In any dendrite the order of a point is equal to the number of components of .
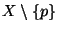4. The set of all end points of a dendrite is 0-dimensional.
5. The set of all end points of a dendrite is a 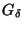-set.
6. The set of all ordinary points (i.e., points of order 2) of a dendrite is dense in .
7. Every dendrite has at most countably many ramification points.
8. If 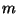is the order of a ramification point in a dendrite, then .
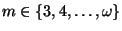9. No dendrite contains points of orde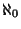r or 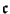(i.e., each dendrite is a regular continuum).

10. In any dendrite the set of all its end points is dense if and only if the set of all its ramification points is dense.

11. Dendrites are absolute retracts. In fact, the class of all 1-dimensional absolute retracts coincide with the class of dendrites, [Borsuk 1967, Corollary 13.5, p. 138].

12. A continuum is a dendrite if and only if for every compact space (continuum) 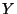and for every light confluent mapping 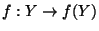such that 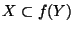there is a copy 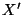of in 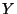for which the restriction 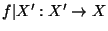is a homeomorphism, [Charatonik et al. XXXXb].

Here you can find source files of this example.

Here you can check the table of properties of individual continua.

Here you can read Notes or write to Notes ies of individual continua.