Řešení obecné kubické rovnice
Řešíme obecnou kubickou rovnici tvaru (kde
![]() je různé od 0, jinak by to nebyla kubická rovnice):
je různé od 0, jinak by to nebyla kubická rovnice):
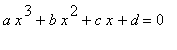 resp.
resp.
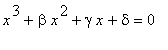 ,
,
to po vydělení rovnice číslem
![]() , přičemž
, přičemž
![]() ,
,
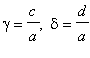 . Další úpravou je možné se "zbavit" i členu s druhou mocninou, zavedením nové proměnné
. Další úpravou je možné se "zbavit" i členu s druhou mocninou, zavedením nové proměnné
![]() vztahem
vztahem
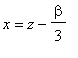 .
.
Dosazením do rovnice pro x dostaneme po úpravě:
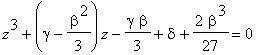
Položíme-li tedy
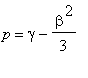 ,
,
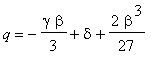
obdržíme tzv. redukovanou kubickou rovnici
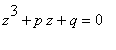 .
.
Řešení této rovnice budeme hledat ve speciálním tvaru
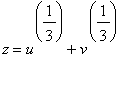 ,
,
kde u, v jsou neznámá (hledaná) čísla. Proč vlastně v tomto tvaru? Jednak proto, že to vyjde :) a jednak to přece jenom má jakousi logiku: očekáváme, že hledané kořeny budou mít co do činění s nějakou kombinací třetích odmocnin, a toto je jedna z nejjednodušších.
Po dosazení a úpravě dostaneme
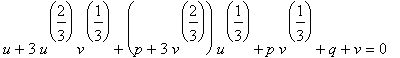
což po úpravě dává
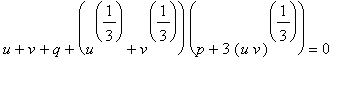 .
.
Tato rovnice bude splněna například tehdy, když
![]()
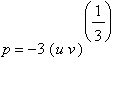
Uvedená soustava pro neznámé
![]() vede na kvadratickou rovnici například pro proměnnou
vede na kvadratickou rovnici například pro proměnnou
![]() : po dosazení
: po dosazení
![]() do druhé rovnice dostaneme
do druhé rovnice dostaneme
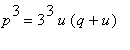 , neboli:
, neboli:
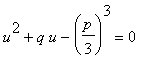 .
.
Diskriminant této kvadratické rovnice,
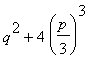 , se nazývá i diskriminantem původní kubické rovnice, častěji se však tímto termínem označuje jeho čtvrtina:
, se nazývá i diskriminantem původní kubické rovnice, častěji se však tímto termínem označuje jeho čtvrtina:
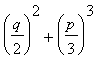 , vyznačující se hezkou symetrií.
, vyznačující se hezkou symetrií.
Problém je tím v podstatě vyřešen,
![]() spočteme jako (stačí jeden) kořen uvedené kvardatické rovnice a
spočteme jako (stačí jeden) kořen uvedené kvardatické rovnice a
![]() najdeme z u. Dosazením získáme i
najdeme z u. Dosazením získáme i
![]() , a po provedení zpětných substitucí se dozvíme i
, a po provedení zpětných substitucí se dozvíme i
![]() . Všecko to pak vypadá takto (proveďte si podrobně):
. Všecko to pak vypadá takto (proveďte si podrobně):
![]()
![]()
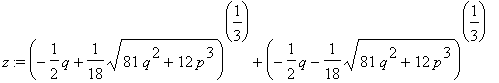
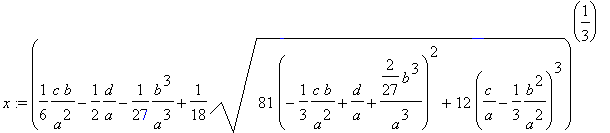
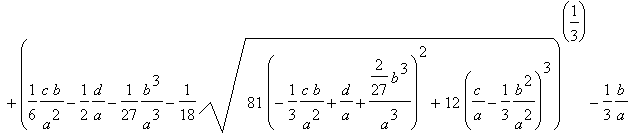
Poslední vyjádření x lze ještě drobně upravit:
![[Maple OLE 2.0 Object]](images/kubicka34.gif)
Tento Cardanův vzorec umožňuje nalézt všechny tři kořeny původní kubické rovnice tím, že bereme do úvahy různé třetí odmocniny výrazů v něm uvedených.
Všechno bylo sepsáno v Maplu (který za mě upravoval výrazy, proto jsem to v něm taky psal), který se vyznačuje nepříliš hezkou úpravou, za kterou se omlouvám.