Cvičení₅

Rozhodněte, zda existuje unární operace ${}'$ a prvek $e$ takové, aby následující čtveřice byly grupami:

$(\Z, -, {}', e)$,
$(\Q\setminus\{0\}, *, {}', e)$, kde $a * b = |a \cdot b|$,
$(\mathcal P(X), \Delta, {}', e)$, kde $\mathcal P(X)$ je množina všech podmnožin množiny $X$ a $\Delta$ je symetrická diference: $A\mathbin{\Delta}B = (A \cup B) \setminus (A \cap B)$.

Ne, odčítání není ani asociativní.

Ne, protože výsledek $*$ je vždy nezáporný, takže pro záporná čísla nenajdeme neutrální prvek.

Ano, položíme-li $A' = A$ (každý prvek bude svým vlastním inverzem) a $e = \emptyset$.

Posloupnost prvků $g^0, g^1, g^2, g^3, \ldots$ musí jednou nabýt nějaké „hodnoty“, která se v ní vyskytuje už dříve (proč?). Jaká ta hodnota bude?

Posloupnost prvků $g^0, g^1, g^2, g^3, \dots$ musí jednou nabýt nějaké „hodnoty“, která se v ní vyskytuje už dříve, protože je $G$ konečná množina; nechť tedy $g^m = g^n$ pro $m < n \in \N_0$ a $n$ je první takové. Pokud by bylo $m > 0$, přenásobením $g^{-1}$ bychom dostali $g^{m-1} = g^{n-1}$, což je spor s minimalitou $n$. Tedy $m = 0$ a $g^n = g^0 = 1$.

Nechť $(G, \odot, {}^{-1}, 1)$ je konečná grupa a $H$ neprázdná podmnožina $G$. Dokažte, že $H$ tvoří podgrupu $G$ právě tehdy, když je uzavřená na operaci $\odot$ (tj. $\forall x, y \in H\colon x \odot y \in H$).
Uveďte příklad grupy a její neprázdné podmnožiny uzavřené na grupovou operaci, která ovšem netvoří podgrupu.

Potřebujeme ukázat, že $H$ je uzavřená i na $^{-1}$ a obsahuje $1$. Víme-li o $g \in G$, že $g^n = 1$ pro nějaké $n \in \N$, co nám to říká o $g^{n-1}$?

Dle (a) je $G$ nezbytně nekonečná grupa, dokonce podle důkazu (a) ani nemůže mít všechny prvky konečného stupně. Máme-li prvek nekonečného stupně, už se příslušná podmnožina $H$ vyrobí snadno…

Jelikož je $H$ uzavřená na operaci $\odot$, obsahuje s každým $h \in H$ i $h^n$ pro všechna $n \in \N$. Jelikož je $G$ konečná grupa, dle předchozí úlohy můžeme pro každé $h \in H$ najít $n \in \N$ takové, že $h^n = 1$. Toto lze přepsat jako $h \odot h^{n-1} = 1$, takže $h^{n-1} = h^{-1}$ (jednoznačnost inverzů), tedy $h^{-1} \in H$. Samozřejmě potom také $1 = h \odot h^{-1} \in H$.

Např. $G = \Z$ se sčítáním atd., $H = \N$. Obecně, máme-li v nějaké grupě prvek $h$ nekonečného řádu, pak můžeme za $H$ vzít $\{h^1, h^2, h^3, \ldots\}$.

Rozepište si, co přesně je $(g \odot h)^n$, a využijte, že inverzy jsou v grupách oboustranné.

Pro $n = 1$ je to známá vlastnost, pro $n > 1$ si napišme $1 = (g \odot h)^n = g \odot h \odot (g \odot h)^{n-1}$, takže také $1 = h \odot (g \odot h)^{n-1} \odot g = (h \odot g)^n$.

Řekneme, že $(K, /, 1)$ je křupa, je-li $K$ množina, $/$ binární operace na $K$ a $1$ prvek $K$, přičemž toto všechno musí splňovat axiomy

$x/1 = x \quad \forall x \in K$,
$x/x = 1 \quad \forall x \in K$,
$(x/z)/(y/z) = x/y \quad \forall x, y, z \in K$.

Navíc se křupa zove kainovská, pokud (opraveno 20. 3.) $(1/x)/y = (1/y)/x$ pro všechna $x, y \in K$. Nahlédněte, že křupy jsou jenom převlečené grupy a kainovské jsou ty abelovské.

Tady. Mimochodem, jak se praví výše na oné stránce, grupu bychom mohli převléct ještě úsporněji. Ve skutečnosti by stačila dvojice $(G, /)$, kde $/$ pro všechna $x, y, z \in G$ splňuje $x / ((((x / x) / y) / z) / (((x / x) / x) / z)) = y$, jak se tvrdí například zde. Jen pak nastanou trable s prázdnou množinou…

„Školní“ příklady grup

Varování: Co někteří autoři značí $\D_n$ (kde $n$ je počet vrcholů pravidelného $n$-úhelníka), jiní značí $\D_{2n}$ (kde $2n$ je počet prvků oné grupy). Zde se budu držet značení z textu, tj. $\D_{2n}$.

Kdykoliv píšu $\Z_n$ nebo $\Z$, myslím tím příslušnou grupu se sčítáním (pokud není řečeno jinak).

Dle Tvrzení 1.4 z textu jsou permutace v $\S_n$ konjugované právě tehdy, když mají stejný typ, což je zjevně relace ekvivalence. Důkaz, který bude fungovat i pro $\A_n$ (a úplně každou grupu), je následující. Reflexivita je zřejmá. Je-li $\varrho \circ \pi \circ \varrho^{-1} = \sigma$, pak $\pi = \varrho^{-1} \circ \sigma \circ (\varrho^{-1})^{-1}$, takže platí symetrie. Konečně, je-li $\varrho \circ \pi \circ \varrho^{-1} = \sigma$ a $\nu \circ \sigma \circ \nu^{-1} = \tau$, pak $(\nu \circ \varrho) \circ \pi \circ (\nu \circ \varrho)^{-1} = \tau$, takže máme i tranzitivitu.

Řád permutace se rovná nejmenšímu společnému násobku délek cyklů. Konjugované permutace mají tytéž délky cyklů (i v $\A_n$), tedy mají i stejný řád.

Třeba $(1\,2)$ a $(1\,2)(3\,4)$ mají obě řád $2$, ale nejsou konjugované, jelikož nemají stejný typ.

Jaký řád mají následující prvky?

$(1\,2\,3\,4)(5\,6\,7)(8\,9)$ v $\S_9$,
$(1\,2\,3\,4)(5\,6\,7)(8\,9)$ v $\A_{2020}$,
$4$ a $15$ v $\Z$,
$4$ a $15$ v $\Z_{75}$,
rotace o $144^\circ$ v $\D_{10}$,
rotace o $144^\circ$ v $\D_{20}$,
prvek $k$ v kvaternionové grupě $\QQ$, (Poznámka: grupa $\QQ$ je podlě mě v textu definována velmi špatně. Zaprvé vůbec není jasné, co se myslí zápisem $-(xy)$ (je to $(-1)xy$? $xy(-1)$? „mínus ten prvek“, co dostanu po vyhodnocení $xy$?), zadruhé ať už ten zápis znamená cokoliv, určitě platí jen pro všechna různá $x, y \in \{i, j, k\}$. Držte se definice z Wikipedie.)
matice (i) $\begin{pmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0\end{pmatrix}$, (ii) $\begin{pmatrix}-1 & 0 & 0 \\ 0 & -\frac12 & -\frac{\sqrt3}2 \\ 0 & \frac{\sqrt3}2 & -\frac12\end{pmatrix}$, (iii) $\begin{pmatrix}1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 2\end{pmatrix}$ a (iv) $\begin{pmatrix}0 & 0 & i \\ 0 & -1 & 0 \\ 1 & 0 & 0\end{pmatrix}$ v $\GL_3(\C)$,
dvojice $\bigl((1\,2\,3)(4\,5), (1\,2\,3\,4)\bigr)$ v direktním součinu $\S_5 \times \S_4$.

Řád permutace je nejmenší společný násobek délek jejích cyklů, tedy $\nsn(4, 3, 2) = 12$.

Všechno kromě $0$ má v $\Z$ řád $\infty$, $4$ a $15$ nejsou výjimkou.

Hledáme nejmenší $n \in \N$, aby $4n$, resp. $15n$ bylo dělitelné $75$, tj. „jednotka“ v aditivní grupě $\Z_{75}$. To je $75$, resp. $5$.

Postupným skládáním rotace o $144^\circ$ dostáváme rotace o $288^\circ$, $432^\circ = 72^\circ$, $576^\circ = 216^\circ$ a konečně $720^\circ = 0^\circ$. Řád je tedy pět.

Podle definice $\QQ$ a jejích prvků z textu platí $k^2 = -1$. Dle Lagrangeovy věty musí řád prvku dělit řád grupy, který je v tomto případě $8$, takže bude $\ord(k)$ buď $4$, nebo $8$ (speciálně to tedy rozhodně nebude $3$). Je $(-1)^2 = 1$, takže $k^4 = 1$ a hledaný řád je tedy $4$.

(i) Daná matice je permutační odpovídající trojcyklu a násobení permutačních matic odpovídá skládání permutací, řád je tedy $3$.

(ii) Daná matice je bloková, při mocnění se bude zvlášť mocnit horní blok $1 \times 1$ a spodní blok $2 \times 2$. Spodní blok odpovídá rotaci o $120^\circ$, tedy jeho třetí mocnina bude jednotková matice $2 \times 2$. Horní blok se při mocnění jednoduše přepíná mezi $1$ (sudé mocniny) a $-1$ (liché mocniny). Vidíme, že oba bloky budou jednotkové „nejdříve“ po umocnění na $\nsn(2, 3) = 6$, což je hledaný řád.

(iii) To, že má matice konečný řád $n$, znamená, že „je kořenem“ polynomu $x^n - 1$ (podobně jako v Hamilton-Cayleyho větě). Kořeny tohoto polynomu musí ovšem být i všechna vlastní čísla této matice. Zadaná matice má zjevně vlastní čísla $1$ a $2$, přičemž $2$ není kořenem $x^n - 1$ pro žádné $n \in \N$. Řád této matice je tedy $\infty$.

(iv) Tak pravila Mathematica:

Řád je tedy $8$.

Je vskutku snadné si rozmyslet, že řád dvojice prvků v direktním součinu je nejmenší společný násobek řádů oněch dvou prvků. Řád $(1\,2\,3)(4\,5)$ v $\S_5$ je $6$, řád $(1\,2\,3\,4)$ v $\S_4$ je $4$, tedy řád zadaného prvku v $\S_5 \times \S_4$ je $\nsn(6, 4) = 12$.

Doplňte následující tabulku, kde v buňce v řádku $k$ a sloupci $\G_n$ bude nejmenší $n \in \N$ takové, že grupa $\G_n$ bude obsahovat prvek řádku $k$. Raději předpokládejte, že $\D_{2n}$ je definováno jen pro $n \geq 3$. \[\begin{array}{c|c|c|c|c|c|} & \S_n & \Z_n & \D_{2n} & \GL_n(\R) & \GL_n(\C) & \SL_n(\C) \\ \hline 2 &&&&&& \\ \hline 4 &&&&&& \\ \hline 11&&&&&& \\ \hline 12&&&&&& \\ \hline 1024&&&&&& \\ \hline \end{array}\]

Řád permutace je nejmenší společný násobek délek cyklů. Kromě $12$ jsou všechny hodnoty mocniny prvočísla, takže je lze dostat jako nsn jen takové sady čísel, která už ono číslo obsahuje, takže příslušná permutace musí mít cyklus této délky. S výjimkou $12$ tedy je odpovědí vždy zadané číslo. $12$ zjevně nedostaneme „úsporněji“ než jako $\nsn(3, 4)$, takže hledaná permutace musí mít jeden cyklus délky $4$ a jeden délky $3$. Na to potřebujeme alespoň $\S_7$, kde tedy takovým prvkem je třeba $(1\,2\,3\,4)(5\,6\,7)$.

$\Z_n$ neobsahuje žádné prvky řádu většího než $n$; na druhou stranu, obsahuje aspoň jeden prvek řádu $n$ (jedničku). Do onoho sloupce tedy vyplníme přesně ta zadaná čísla $k$.

$\D_{2n}$ obsahuje k rotacím navíc jen osové symetrie, které mají všechny řád $2$, takže nám v ničem nepomohou. Rotaci řádu $n$ bude mít za symetrii „jako první“ vždy pravidelný $n$-úhelník, takže s výjimkou prvního řádku, kam z definitorických důvodů doplníme $3$, doplníme do ostatních přesně zadáná čísla. (Ale můžete se zamyslet nad tím, co je to takový dvojúhelník a jaké jsou jeho symetrie.)

Prvek řádu $2$ se vyskytuje už v $\GL_1(\R)$, je to $1 \times 1$ matice $(-1)$. To je ale jediný netriviální prvek $\GL_1(\R)$ konečného řádu. Libovolný další řád už ale nalezneme v $\GL_2(\R)$: matice otočení o $360^\circ/n$ má přesně řád $n$. Mimochodem, tyto matice jsou dokonce prvky $\SL_2(\R)$.

Prvek libovolného konečného řádu nalezneme už v $\GL_1(\C)$, bude to $1 \times 1$ matice $(\mathrm{e}^{2\pi i/n})$.

Chceme-li mít determinant roven jedné, s $\SL_1(\C)$ si nevystačíme (je to triviální grupa). Můžeme ale v $\SL_2(\C)$ použít tytéž matice, co jsme použili v $\GL_2(\R)$, nebo třeba (jim podobné) matice $\begin{pmatrix}\mathrm{e}^{2\pi i/n} & 0 \\ 0 & \mathrm{e}^{-2\pi i/n} \end{pmatrix}$.

\[\begin{array}{c|c|c|c|c|c|} & \S_n & \Z_n & \D_{2n} & \GL_n(\R) & \GL_n(\C) & \SL_n(\C) \\ \hline 2 & 2 & 2 & 3 & 1 & 1 & 2 \\ \hline 4 & 4 & 4 & 4 & 2 & 1 & 2 \\ \hline 11& 11 & 11 & 11 & 2 & 1 & 2 \\ \hline 12& 7 & 12 & 12 & 2 & 1 & 2 \\ \hline 1024& 1024 & 1024 & 1024 & 2 & 1 & 2 \\ \hline \end{array}\]

Multiplikativní grupa toho menšího tělesa by byla podgroupu multiplikativní grupy toho většího.

Multiplikativní grupa toho menšího tělesa by byla podgroupu multiplikativní grupy toho většího, jelikož podtěleso je uzavřené na násobení a multiplikativní inverzy a obsahuje jednotkový prvek. Ovšem těleso o $27$ prvcích má multiplikativní grupu řádu $26$, pročež těleso o $9$ prvcích má multiplikativní grupu řádu $8$. Jelikož $8$ nedělí $26$, nemůže dle Lagrangeovy věty být ta menší grupa podgrupou té větší.

Sčítací grupa $\Z_2 \times \Z_2$ se mnohdy označuje jako Kleinova čtyřgrupa, značená $\V$; obecně, jde o komutativní grupu řádu $4$, kde má každý netriviální prvek řád $2$. „Kopii“ této grupy můžeme nalézt jako podgrupu v mnoha jiných grupách.

Nalezněte kopii $\V$ jako podgrupu $\S_n$ pro $n \geq 4$.
Ukažte, že $\S_3$ neobsahuje $\V$ jako podgrupu.
Ukažte, že $\Z_n$ neobsahuje $\V$ jako podgrupu pro žádné $n \in \N$.
Ukažte, že $\D_{2n}$ obsahuje $\V$ jako podgrupu právě tehdy, když je $n$ sudé.
Ukažte, že pro žádné těleso $\kk$ neobsahuje jeho multiplikativní grupa $\kk^*$ $\V$ jako podgrupu.
Nalezněte nějaké $n \in \N$ takové, že grupa $\Z_n^*$ invertibilních prvků okruhu $\Z_n$ obsahuje $\V$ jako podgrupu.
☺ Kleinova čtyřgrupa se může hodit, když chcete napsat třeba nějakou fugu. Vyjdete z nějakého motivu (tzv. prime), který můžete následně přepsat pozpátku (retrograde), překlopit v notách podle vodorovné osy (inversion), nebo provést oboje (retrograde inversion); pardon, českou terminologii neznám. Praktickou ukázku naleznete třeba v tomto videu plném vlasatých pánů a inteligentního humoru.

Je to třeba $\{\mathrm{id}, (1\,2), (3\,4), (1\,2)(3\,4)\}$.

$\S_3$ má řád $6$, $\V$ má řád $4$, dle Lagrangeovy věty to nemůže být podgrupa.

Grupa $\Z_n$ obsahuje nanejvýš jeden prvek řádu $2$ – tím je $n/2$, pokud je $n$ sudé.

Je-li $n$ liché, pak $|\D_{2n}| = 2n$ není dělitelné čtyřmi, takže dle Lagrangeovy věty nemůže mít jako podgrupu $\V$. Je-li $n$ sudé, pak je příslušná podgrupa tvořena identitou, rotací o $180^\circ$ a osovými symetriemi podle dvou na sebe kolmých os.

Všechny tři netriviální prvky $\V$ by (jakožto prvky $\kk$) musely splňovat $x^2 = 1$, to mohou ale nejvýše dva různé prvky $\kk$.

Třeba $n = 8$; pak $\Z_8^* = \{1, 3, 5, 7\}$ je zřejmě komutativní a platí $3^2 = 5^2 = 7^2 = 1$ (takže je to dokonce přímo $\V$).

Očíslujme v nějakém pořadí všech deset prvků dihedrální grupy $\D_{10}$ ciframi $0,\ldots,9$.

Rozmyslete si, že pokud máme řetězec cifer, můžeme ho jednoznačně doplnit (třeba zprava) jednou „kontrolní“ cifrou tak, aby se odpovídající řetězec prvků $\D_{10}$ vynásobil na jednotkový prvek (identickou symetrii). Nazvěme takové řetězce platné.
Rozmyslete si, že pokud ve výsledném řetězci na jednom místě cifru změníme, přestane být platný.
Rozmyslete si, že toto pravidlo pozná i některá prohození sousedních cifer. Spočtěte pravděpodobnost, že pokud první dvě cifry řetězce zvolíme náhodně (nezávisle na sobě s rovnoměrným diskrétním rozdělením), řetězec doplníme na platný a posléze ony dvě cifry prohodíme, bude řetězec stále platný. Potenciálně může pomoct toto, kde jsou prvky $\D_{10}$ vypsány jako permutace na vrcholech; není těžké nahlédnout, že dvě permutace komutují právě tehdy, když konjugace jednou nezmění tu druhou.

Poznámka: s pomocí $\D_{10}$ lze vyrobit i algoritmus na kontrolní cifru, která odhalí všechny chyby v jedné cifře i všechna prohození sousedních cifer (Verhoeff algorithm).

Jako poslední prvek doplníme inverzní prvek k součinu všech předchozích prvků.

Nechť (prvek $\D_{10}$) $x$ jsme nahradili za $y$ a nechť součin prvků v řetězci vlevo od $x$ byl $l$ a vpravo od $x$ byl $r$. Pak $r \odot x \odot l = r \odot y \odot l$, ale protože v grupách se dá krátit z obou stran, dostáváme $x = y$, tedy řetězec zůstane platný jen tehdy, když nahradíme nějakou cifru sebou samotnou.

Chceme znát počet dvojic $(x, y) \in \D_{10} \times \D_{10}$ splňujících $x \odot y = y \odot x$. Budeme za $x$ brát postupně všechny prvky $\D_{10}$ a spočteme, kolik $y \in \D_{10}$ s nimi komutuje. Pro triviální prvek to jsou všechny ($1 \cdot 10$ dvojic). S libovolnou netriviální rotací komutují právě všechny rotace (včetně triviální) ($4 \cdot 5$ dvojic). Se symetrií podle nějaké osy komutuje jen ona sama a identita ($5 \cdot 2$ dvojic). (Vlastně jsme počítali, kolik políček zůstane stejně obarvených, pokud tabulku zde transponujeme.) Pravděpodobnost toho, že řetězec zůstane platný, tedy je $40/100 = 2/5$.

★ A teď ty zajímavé grupy

Volná grupa na $X$ (kde $X$ je libovolná množina) je jakožto množina tvořena všemi (konečnými) řetězci (též slovy) tvaru $a_1^{\varepsilon_1}a_1^{\varepsilon_2}a_3^{\varepsilon_3}\cdots a_n^{\varepsilon_n}$, kde $a_i \in X$ a $\varepsilon_i \in \{\pm 1\}$, přičemž zakazujeme, aby vedle sebe byly $a$ a $a^{-1}$ (pro totéž $a$). Připouštíme i prázdný řetězec. Typický prvek volné grupy na $\{a, b\}$ vypadá třeba nějak takto: $aaab^{-1}b^{-1}abba^{-1}b$. Grupové násobení definujeme tak, že řetězce napíšeme za sebe a pokud tím vzniknou „zakázané podřetězce“ tvaru $a^{-1}a$ nebo $aa^{-1}$, tak tyto odstraňujeme tak dlouho, dokud se všech nezbavíme. Inverzní řetězec se dostane tak, že všechny exponenty změníme a obrátíme pořadí, takže invers třeba k tomu vzorovému prvku je $b^{-1}ab^{-1}b^{-1}a^{-1}bba^{-1}a^{-1}a^{-1}$. Jednotkou je prázdný řetězec.

Nahlédněte, že volná grupa generovaná jedním prvkem je v podstatě totéž co $\Z$.
Dokažte, že každý netriviální prvek volné grupy má nekonečný řád.

Více o volných grupách v dalších sadách…
Poznámka: Volná grupa je klíčovou ingrediencí v Banach-Tarského paradoxu.

Lehce filozofické okénko: v minulém díle jsme symetrie chápali jako isometrie. Jinak řečeno, šlo nám o bijekce, které zachovají vlastnosti objektu, přičemž v tomto případě byly oněmi vlastnostmi metrické vlastnosti. Následující úlohy demonstrují, že ony vlastnosti mohou být rozličné matemamatické povahy.

Máme-li graf $G$, pak množina jeho automorfismů $\Aut(G)$ (tj. takových permutací množiny vrcholů, které pošlou vrcholy spojené hranou na vrcholy spojené hranou) tvoří přirozeným způsobem grupu: násobení je skládání zobrazení, inverzem je inverzní zobrazení a jednotkou je identické zobrazení. Grafem zde myslíme ten úplně „nejobyčejnější“ typ grafu (žádné smyčky, neorientované hrany, bez násobných hran).

Co je grupa automorfismů úplného grafu $K_n$?
Co je grupa automorfismů úplného grafu $K_n$, ze kterého odebereme jednu hranu?
Co je grupa automorfismů kružnice $C_n$?
Co je grupa automorfismů úplného bipartitního grafu $K_{m,n}$?
Co je grupa automorfismů Petersenova grafu, který můžeme chápat tak, že vrcholy jsou dvouprvkové podmnožiny $\{1,\dots,5\}$, které jsou spojeny hranou právě tehdy, když jsou junktní?
Nalezněte graf s alespoň dvěma vrcholy, který bude mít triviální grupu automorfismů.
Nalezněte graf, jehož grupa automorfismů bude Kleinova čtyřgrupa.
Pro $n \in \N$ nalezněte graf, jehož grupa automorfismů bude $\Z_n$.

$\S_2 \times \S_{n-2}$

Je-li $m \neq n$, pak $\S_m \times \S_n$, je-li $m = n$, tak $\S_m \times \S_n \times \S_2$ (můžeme prohodit partity).

$\S_5$, jsou to přesně permutace té množiny $\{1, \dots, 5\}$.

Třeba strom o sedmi vrcholech, kde z „centrálního“ vrcholu stupně $3$ budou vycházet větve délky $1$, $2$ a $3$.

Nakreslete si kosočtverec… a doplňte vhodnou diagonálu!

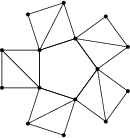
Takto nějak to je pro $n = 5$:

Analogicky k předchozí úloze si rozmyslete, že automorfismy okruhu tvoří grupu.
Je-li $R$ okruh a $S$ jeho podokruh, nahlédněte, že ty automorfismy, které se chovají jako identita na $S$, tvoří podgrupu $\Aut(R)$.
Nahlédněte, že každý automorfismus tělesa je identitou na jeho prvotělese.
Co je grupa těch automorfismů tělesa $\C$, které jsou identitou na $\R$?
Co je grupa těch automorfismů tělesa $\Q(\sqrt[3]2)$, které jsou identitou na $\Q$?

Podobných výpočtů si užijete ještě ažaž u Galoisovy teorie, takže toto by pro dnešek stačilo.

Cvičení₅

Základní vlastnosti grup

„Školní“ příklady grup

★ A teď ty zajímavé grupy