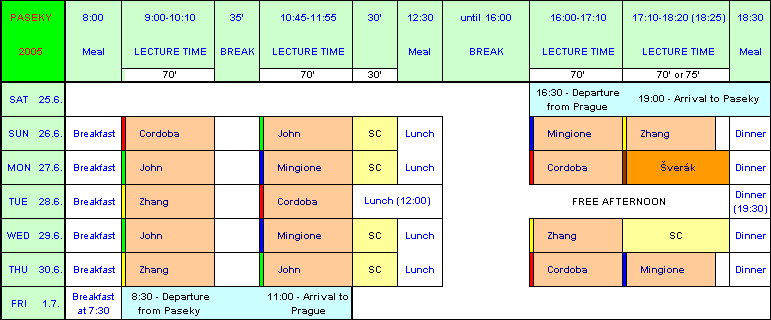
The program of the conference
There will be one "guest one-lecture speaker" on Monday evening
SC = Short Communications of participants (the length depending on number of them)
Abstracts of main lectures
- DIEGO CORDOBA

Instituto de Matematicas y Fisica Fundamental
Consejo Superior de Investigaciones Cientificas
C/Serrano, 123, 28006 Madrid, Spain
email: dcg@imaff.cfmac.csic.es
home: http://www.mat.csic.es/investigadores.phpOn the search for singularities in incompressible flows
Abstract:
The main topic of these lectures will be to discuss the possible formation of singularities in different models of incompressible flows.
- VOLKER JOHN

FR 6.1 - Mathematik
Universitaet des Saarlandes
Postfach 15 11 50, 66041 Saarbruecken, Germany
email: john@math.uni-sb.de
home: http://www-ian.math.uni-magdeburg.de/~john/Numerical simulation of turbulent flows
Abstract:
The numerical simulation of turbulent flows is one of the great challenges in Computational Fluid Dynamics (CFD). In general, a Direct Numerical Simulation (DNS) is not feasible due to limited computer resources (performance and memory) and the use of a turbulence model becomes necessary. The lectures will present Large Eddy Simulation (LES) and Variational Multiscale (VMS) models. Topics which will be addressed are the analysis of commutation errors in LES models, the derivation and the finite element discretization of LES and VMS models, finite element error estimates, issues on the implementation of these models as well as results of numerical simulations.
- GIUSEPPE R. MINGIONE

Dipartimento di Matematica
Universita degli Studi di Parma
Parco Area delle Scieze 53/a (Campus)
43100 PARMA, Italy
email: giuseppe.mingione@unipr.it
home: http://www2.unipr.it/~mingiu36/Regularity topics for elliptic problems: standard and non- standard
Abstract:
I will give a general review of regularity theory for elliptic, possibly variational, problems, starting from the standard partial regularity in the vectorial case and everywhere regularity in the scalar one. I will then pass to examine so called problems with non-standard growth conditions, especially those coming up in non-newtonian fluid-dynamics. Finally I will concentrate on the problem of estimate the size of the singular sets of such problems, talking about positive results and counterexamples.
References:
- Acerbi, E. and Mingione, G.: Regularity results for stationary electro-rheological fluids. Arch. Ration. Mech. Anal. 164 (2002), 213--259.
- Fonseca I., Maly J., and Mingione G.: Scalar minimizers with fractal singular sets - Arch. Ration. Mech. Anal. 172 (2004) 295-312
- Giusti: Direct Methods in the Calculus of Variations. World Scietific 2003.
- Marcellini P.: Regularity and existence of solutions of elliptic equations with $p,q$-growth conditions. J. Differential Equations 90 (1991), 1-30.
- Mingione G.: Bounds for the singular set of solutions to non linear elliptic systems. Calc. Var. 18 (2003) 373-400.
- Sverak, V. and Yan, X.: Non-Lipschitz minimizers of smooth uniformly convex functionals. Proc. Natl. Acad. Sci. USA 99 (2002), 15269-15276.
- PING ZHANG

Academy of Mathematics and System Sciences
Chinese Academy of Sciences
Beijing 100080, P.R. China
email: zp@math03.math.ac.cn
The methods of Young measures and mollifiers
Abstract:
We study an elegant nonlinear wave equation which arises beautifully in a simplified liquid crystal model through the variational principle. The equation appears in several other disciplines as well. A distinctive feature of the equation is that the wave speed depends on the wave amplitude, in addition to its nonconservative appearance that is a natural consequence of the variational principle. We present recent results on the existence and uniqueness of weak solutions for the initial value problems for the equation. Our emphasis is to show the reader the various interesting phenomena that the equation possesses and the modern methods of Young measures, mollifiers, and related techniques. We first present simple asymptotic equations for weakly nonlinear and unidirectional waves of the equation. The asymptotic equations to the nonlinear variational wave equation is what the Burgers equation to hyperbolic systems of conservation laws. We show the existence of two types of weak solutions to the initial value problem for the (first-order) asymptotic equation for data in the natural space of square integrable functions, and we establish the uniqueness of weak solutions for both the dissipative and conservative types.
Enlarged abstract to be found here.
- VLADIMIR SVERAK

School of Mathematics
127 Vincent Hall, 206 Church St. S.E.
Minneapolis, MN 55455, USA
email: sverak@math.umn.edu
home: http://www2.itdean.umn.edu/faculty/detail.jsp?facultyID=349Some recent results in mathematical theory of incompressible flows
... and a guest one-lecture speaker