


Next: Formulation of the Problem
Up: No Title
Previous: Notation
Conservation laws ( the conservation of mass, the
conservation of momentum, the conservation of momentum of momentum and
the conservation of energy), which accompanied by the constitutive
and thermodynamical state equations lead to the system of the
Navier - Stokes equations describing the motion of viscous
compressible flows. The precise mathematical determinatin can be found
in many textbooks, e.g. [#!Feistauer!#] so that we present only the
mathematical formulation of physical conservation laws:
The conservation law of density has the form
| 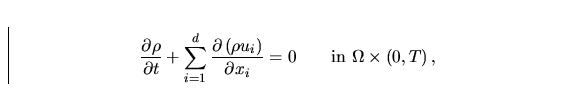 |
(1) |
the conservation law of momentum
| 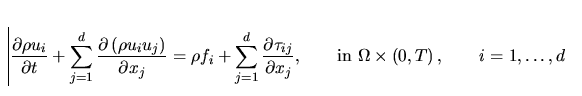 |
(2) |
and the conservation of energy
| 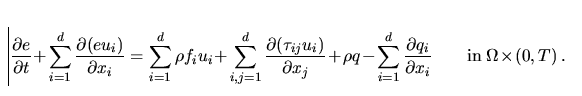 |
(3) |
Further form the conservation of momentum of momentum we derive
that stress tensor 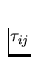 is symmetric, i.e.
is symmetric, i.e.
 .
.
We see that the number of unknown quantities is larger than the
number of
equations. To complete the whole system of conservation laws we have to
add some constitutive or closing equations
that will specify our fluids. At first we must find relation between
the stress tensor 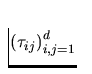 and other
quantities describing the fluid motion. We will suppose Newtonian fluid
for which stress tensor can be evaluated in the form
and other
quantities describing the fluid motion. We will suppose Newtonian fluid
for which stress tensor can be evaluated in the form
| 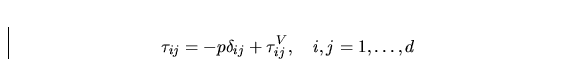 |
(4) |
where  is the Kronecker delta and
is the Kronecker delta and
 is the so called deformation velocity
tensor
is the so called deformation velocity
tensor
| 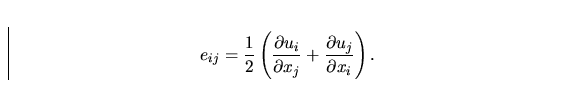 |
(5) |
Here  are viscosity coefficients. For them we will use
the relation derived from the kinetic theory for the one-atomic gas:
are viscosity coefficients. For them we will use
the relation derived from the kinetic theory for the one-atomic gas:
| 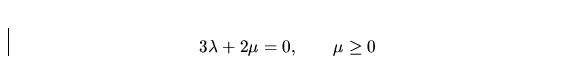 |
(6) |
The next constitutive relation is obtained from Fourier's law
| 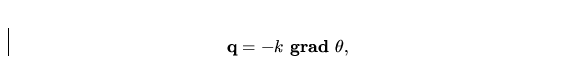 |
(7) |
where  is called the heat conductivity and is supposed to be
constant.
is called the heat conductivity and is supposed to be
constant.
We will always consider the perfect gas, which means
| 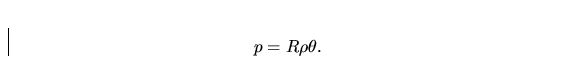 |
(8) |
This equation is called the state equation of the perfect gas.
R>0 is
the specific gas constant and it can be expressed in the form
where cp and cv are the specific heat at constant pressure and
volume, respectively. We assume that cp and cv are constants. It
follows from theory that cp>cv. The quantity
| 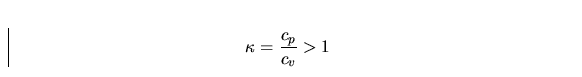 |
(10) |
is called the Poisson constant.
The total energy e consists of the internal energy
u and the kinetic energy. We suppose the perfect polytropic gas, i.e.
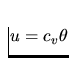 . We obtain
. We obtain
| 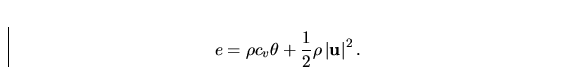 |
(11) |
Now putting (4), (5), (8), (12)
in (1), (2)
and (3) we obtain
| 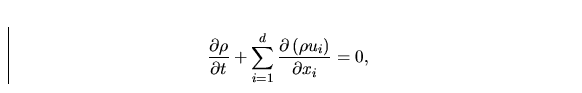 |
(12) |
| 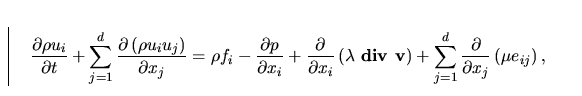 |
(13) |
Now together with (9) we have the closed system for the unknowns
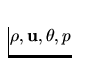 .
.



Next: Formulation of the Problem
Up: No Title
Previous: Notation
Vit Dolejsi
12/17/1998
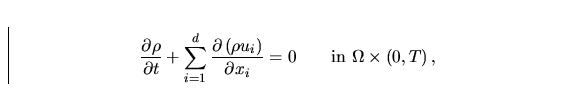
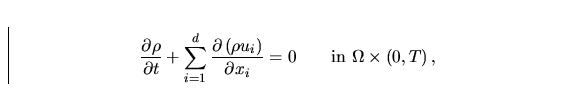
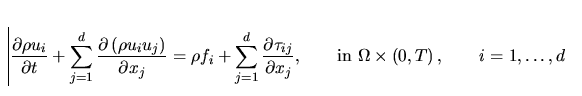
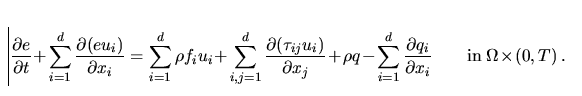
![]() is symmetric, i.e.
is symmetric, i.e.
 .
.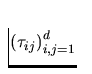 and other
quantities describing the fluid motion. We will suppose Newtonian fluid
for which stress tensor can be evaluated in the form
and other
quantities describing the fluid motion. We will suppose Newtonian fluid
for which stress tensor can be evaluated in the form
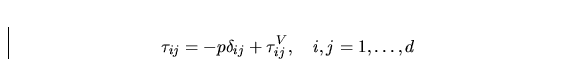

 is the so called deformation velocity
tensor
is the so called deformation velocity
tensor
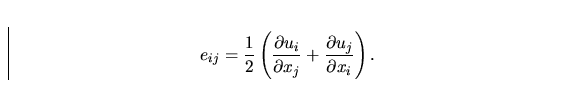
 are viscosity coefficients. For them we will use
the relation derived from the kinetic theory for the one-atomic gas:
are viscosity coefficients. For them we will use
the relation derived from the kinetic theory for the one-atomic gas:
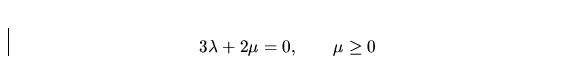
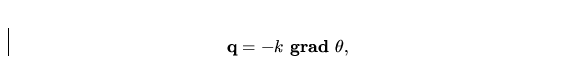
 is called the heat conductivity and is supposed to be
constant.
is called the heat conductivity and is supposed to be
constant.
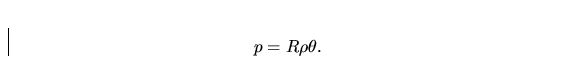
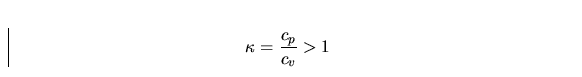
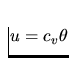 . We obtain
. We obtain
 .
.