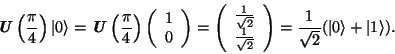


Next: Kvantová interference
Up: Stručný přehled kvantové mechaniky
Previous: Kvantový registr
Obsah
Vývojem (evolucí) kvantového systému máme na mysli jeho změnu s časem.
Nyní je důležité připomenout, že právě zde je zásadní rozdíl mezi
pozorovaným a nepozorovaným systémem. V případě, že jej nepozorujeme,
podléhá stavový vektor spojitému vývoji, který jednoznačně popisuje
s tímto systémem související Schrödingerova vlnová rovnice:
Abychom však mohli kvantový systém matematicky ovlivňovat, je zapotřebí
definovat vhodné operátory. V kvantové mechanice jsou však dovoleny pouze
některé způsoby vývoje systému. Jmenovitě jde o takové vývoje, z jejichž
výsledků (výstupů) se dají jedinečně odvodit předchozí stavy (vstupy).
To je podmínka tzv. reverzibility vývoje kvantového stavu, která
plyne z deterministické povahy Schrödingerovy rovnice. Taková
reverzibilita je však matematicky možná jen pokud jsou operátory
čtvercové unitární matice, tj. pokud o takových maticích platí, že
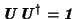 .
Pokud jsou stavové vektory normalizovány a jsou to tedy
body v kouli o poloměru 1, pak unitární kvantový vývoj s těmito body
rotuje. Jestliže provedeme následující úpravy
.
Pokud jsou stavové vektory normalizovány a jsou to tedy
body v kouli o poloměru 1, pak unitární kvantový vývoj s těmito body
rotuje. Jestliže provedeme následující úpravy
lze Schrödingerovu vlnovou rovnici přepsat na
kde
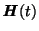 je Hamiltonián. Jak je vidět i z výše uvedené
substituce, je Hamiltonián úzce spjat s energií systému a jeho podoba je
odvozena od fyzického uspořádání částic nebo molekul, z nichž se systém skládá
(mohou ho charakterizovat například veličiny jako síla el.pole nebo směr
molekulového dipólového momentu). Hamiltonián se skládá z vektorů vlastních
stavů a tvoří bázi v Hilbertově prostoru.
Obecně by mohly mít vlastní stavy komplexní vlastní hodnoty, ale protože je
Hamiltonián Hermitová matice (tj.
je Hamiltonián. Jak je vidět i z výše uvedené
substituce, je Hamiltonián úzce spjat s energií systému a jeho podoba je
odvozena od fyzického uspořádání částic nebo molekul, z nichž se systém skládá
(mohou ho charakterizovat například veličiny jako síla el.pole nebo směr
molekulového dipólového momentu). Hamiltonián se skládá z vektorů vlastních
stavů a tvoří bázi v Hilbertově prostoru.
Obecně by mohly mít vlastní stavy komplexní vlastní hodnoty, ale protože je
Hamiltonián Hermitová matice (tj.
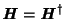 ), mají vlastní stavy garantovány reálné
vlastní hodnoty, které korespondují možným výsledkům měření nějaké fyzikální
veličiny. V Hamiltoniánu jsou, kromě informací o vlastních stavech, obsaženy
informace o všech operacích, které
během výpočtu použijeme. Jestliže uvažujeme Hamiltonián, který není
závislý na čase, tzn. takový, který se po dobu vývoje systému nemění a
paměťový registr je na počátku ve stavu
), mají vlastní stavy garantovány reálné
vlastní hodnoty, které korespondují možným výsledkům měření nějaké fyzikální
veličiny. V Hamiltoniánu jsou, kromě informací o vlastních stavech, obsaženy
informace o všech operacích, které
během výpočtu použijeme. Jestliže uvažujeme Hamiltonián, který není
závislý na čase, tzn. takový, který se po dobu vývoje systému nemění a
paměťový registr je na počátku ve stavu
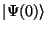 , má vlnová rovnice
řešení
, má vlnová rovnice
řešení
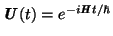 se nazývá časově
závislý evoluční operátor, který je vždy unitární matice. Evoluční
operátor nám tedy ukazuje, jak se systém dynamicky vyvíjí v čase.
Jak by řečeno, v Hamiltoniánu jsou zaznamenány kvantové operace, které
popisují výpočet. K vyjádření takové operace na kvantovém systému nám
postačuje operátor, kterým násobíme příslušný stav. Například operátor
se nazývá časově
závislý evoluční operátor, který je vždy unitární matice. Evoluční
operátor nám tedy ukazuje, jak se systém dynamicky vyvíjí v čase.
Jak by řečeno, v Hamiltoniánu jsou zaznamenány kvantové operace, které
popisují výpočet. K vyjádření takové operace na kvantovém systému nám
postačuje operátor, kterým násobíme příslušný stav. Například operátor
můžeme použít s parametrem
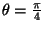 , abychom převedli
systém z vlastního stavu
, abychom převedli
systém z vlastního stavu 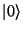 do vyvážené superpozice stavů
do vyvážené superpozice stavů
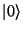 a
a 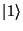 :
:
Z amplitud pravděpodobností vidíme, že stavy jsou opravdu vyvážené a
normalizované, protože
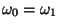 a
a
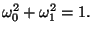 Vraťme se nyní na počátek a připomeňme, že těmito operacemi je možné
systém vyvíjet pouze pokud není pozorován (je dostatečně izolován od
okolí). V případě, že jej však změříme, přejde stochasticky do jednoho z
vlastních stavů podle toho, jaké jsou hodnoty jejich amplitud pravděpodobností
a podle výsledku našeho měření.
Vraťme se nyní na počátek a připomeňme, že těmito operacemi je možné
systém vyvíjet pouze pokud není pozorován (je dostatečně izolován od
okolí). V případě, že jej však změříme, přejde stochasticky do jednoho z
vlastních stavů podle toho, jaké jsou hodnoty jejich amplitud pravděpodobností
a podle výsledku našeho měření.



Next: Kvantová interference
Up: Stručný přehled kvantové mechaniky
Previous: Kvantový registr
Obsah
Bashar
2001-01-23