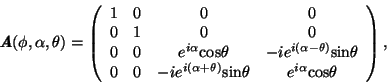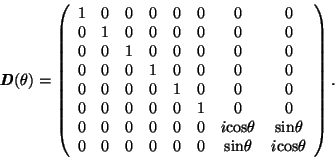


Next: Kvantové algoritmy
Up: Kvantové obvody
Previous: Kvantové brány
Obsah
Na závěr se vraťme k otázce univerzálnosti kvantových bran.
Tak jako existují pro klasické obvody množiny univerzálních operátorů,
je možné i u kvantových počítačů požadovat univerzalitu. Přitom se snažíme,
aby byla tato množina operátorů co nejjednodušší a tím i lépe
implementovatelné. Mezi klasickými branami jsou takovými množinami například
{NAND} nebo {OR, NOT}.
U kvantových bran bylo dokázáno, že Fredkinova a
Toffoliho 3-qubitová brána jsou samy o sobě univerzální7(a velmi obtížné na implementaci, protože bychom museli ovládat interakci mezi
třemi kvantovými systémy). Davidu DiVincenzovi se však podařilo dokázat, že
na rozdíl od klasické informatiky, lze v kvantové informatice vyjádřit
libovolný kvantový obvod pouze s využitím 2-qubitových bran.
Uvažujeme-li 2-qubitovou bránu CNOT8, pak lze dokázat, že
tato brána není samotná univerzální. Může nás však napadnout, že společně s
nějakou 1-qubitovou bránou by taková množina univerzální být mohla (což by bylo
nadějné vzhledem k méně náročné implementaci 1- a 2-qubitových bran). Jak bylo
zjištěno, lze obecnou 1-qubitovou unitární transformaci U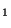 vyjádřit jako součin čtyř matic
vyjádřit jako součin čtyř matic 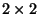
kde první matice je fázový posun vzhledem k 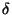 , druhá a čtvrtá matice
jsou rotace o daný úhel kolem
, druhá a čtvrtá matice
jsou rotace o daný úhel kolem 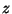 a třetí matice je rotace kolem osy
a třetí matice je rotace kolem osy 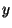 o úhel
o úhel 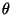 . Po roznásobení dostáváme
. Po roznásobení dostáváme
kde
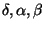 a
a
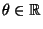 . Například při
. Například při
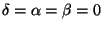 vytvoříme operátor, který mezi sebou prohazuje
qubity
vytvoříme operátor, který mezi sebou prohazuje
qubity
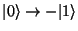 a
a
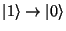 .
Právě pro množinu
{U
.
Právě pro množinu
{U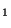
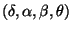 ,
CNOT} Adriano Barenco a jiní dokázali, že je pro konstrukci
kvantových obvodů univerzální. Kombinací těchto dvou bran je totiž možné
vytvořit Toffoliho univerzální bránu.
Navíc lze univerzalitu 2- a 3-qubitových bran v jistém smyslu zobecnit
a vyjádřit jako příslušnou parametrizovanou kvantovou bránu.
Například 2-qubitovou univerzální bránu pro bázi
,
CNOT} Adriano Barenco a jiní dokázali, že je pro konstrukci
kvantových obvodů univerzální. Kombinací těchto dvou bran je totiž možné
vytvořit Toffoliho univerzální bránu.
Navíc lze univerzalitu 2- a 3-qubitových bran v jistém smyslu zobecnit
a vyjádřit jako příslušnou parametrizovanou kvantovou bránu.
Například 2-qubitovou univerzální bránu pro bázi
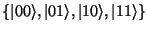 poprvé popsal Adriano
Barenco:
poprvé popsal Adriano
Barenco:
kde
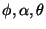 jsou pevně zvolené iracionální násobky
jsou pevně zvolené iracionální násobky 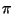 nebo samy sebe. Ještě před Barencem zobecnili reverzibilní Toffoliho bránu
Deutsch a DiVincenzo a pro bázi
nebo samy sebe. Ještě před Barencem zobecnili reverzibilní Toffoliho bránu
Deutsch a DiVincenzo a pro bázi
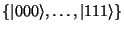 vymysleli 3-qubitovou univerzální bránu.
vymysleli 3-qubitovou univerzální bránu.
Je zřejmé, že
D
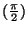 = CCNOT.
= CCNOT.



Next: Kvantové algoritmy
Up: Kvantové obvody
Previous: Kvantové brány
Obsah
Bashar
2001-01-23