

Next: Kvantová teleportace
Up: Kvantové algoritmy
Previous: Kvantová kryptografie
Obsah
V předchozích kapitolách jsme často používali spojení,
že někdo něco náhodně vygeneruje nebo náhodně vybere variantu. Téměř jako bychom
předpokládali, že na náhodných procesech není nic, co by stálo za hlubší
analýzu. Podívejme se však nyní podrobněji na to, co náhodné jevy znamenají
na klasickém počítači a jaké jsou možnosti při jejich realizaci na kvantových
počítačích.
V některých vědních disciplínách se setkáváme s problémy, které
není možné řešit deterministicky a výhodnější je při jejich řešení
použít algoritmů využívajících náhodných čísel, která často vedou k řešení
rychleji. I v algoritmech, o kterých jsme se zmínili, je často nutné
provést náhodnou volbu nebo vygenerovat náhodné číslo. Řekněme si však
nejprve, co to vlastně náhodné číslo je. Matematicky je možné o náhodném čísle
mluvit, pokud je součástí posloupnosti několika čísel nebo číslic,
tj. v určitém kontextu.
V takovém případě můžeme například pomocí zkoušek na distribuci a
korelaci mezi čísly v posloupnosti rozhodnout, zda lze tuto posloupnost
považovat za náhodnou. Protože po klasických počítačích nemůžeme chtít nic
jiného, než aby zpracovávaly algoritmicky vstupy a vracely výstupní data,
lze vždy pouze skončit u lepšího nebo horšího generátoru náhodných čísel.
Jistě si dovedeme
představit posloupnost, která by prošla oběmi výše uvedenými zkouškami,
ale nějaká další zkouška by v posloupnosti odhalila skrytý vzorec. Proto je
problém rozhodnutí o náhodnosti posloupnosti ekvivalentní problému o
bezztrátové kompresibilitě dané posloupnosti (tzv. Kolmogorova-Chaitinova
interpretace). To znamená, že jedině pokud je
posloupnost nezhustitelná do kratší podoby, je opravdu náhodná. Ve skutečnosti
je problém odhalení náhodnosti (kompresibility) posloupnosti
nealgoritmizovatelný, tudíž nevypočitatelný. Z toho rovnou plyne, že není
možné klasicky náhodné číslo vygenerovat; vždy je výstupem jen sekvence čísel,
vytvořená podle určitého předpisu. Proto dokáží klasické generátory produkovat
jen tzv. pseudonáhodná čísla. Ta překvapivě pro řadu problémů postačují, ne
však pro všechny.
Abychom měli co srovnávat, podívejme se nyní stručně na některé klasické
generátory náhodných čísel a posuďme, jak kvalitní výsledky vracejí.
První známou skupinou jsou lineárně-kongruentní generátory založené na
výpočtu pravidla:
kde 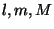 jsou celočíselné parametry. Pokud
jsou celočíselné parametry. Pokud
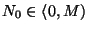 , pak
toto pravidlo generuje čísla z rozsahu
, pak
toto pravidlo generuje čísla z rozsahu
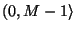 . Výstupy těchto
generátorů jsou náhodné, avšak periodické s periodou nejvýše
. Výstupy těchto
generátorů jsou náhodné, avšak periodické s periodou nejvýše 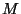 . Perioda
je ale velmi závislá na volbě parametrů. Špatná volba znamená malou
periodu a časté opakování stejných čísel. Lineárně-kongruentní generátor
používá s parametry
. Perioda
je ale velmi závislá na volbě parametrů. Špatná volba znamená malou
periodu a časté opakování stejných čísel. Lineárně-kongruentní generátor
používá s parametry
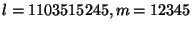 a
a 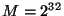 například UNIXová
funkce rand() generující 32-bitová celá čísla. Pro aplikace používající
32-bitový int jsou však někdy tyto generátory nedostatečné, protože
perioda
například UNIXová
funkce rand() generující 32-bitová celá čísla. Pro aplikace používající
32-bitový int jsou však někdy tyto generátory nedostatečné, protože
perioda
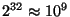 , může být na dnešních počítačích vyčerpána za
několik sekund. Aritmetika s dvojtou šířkou, pak může být neúnosně pomalá.
Další nevýhodou se později ukázala skutečnost, že skupiny generovaných čísel
vykazují geometrický vzorec, který odhaluje test na prostorové rozložení
(scatter plot test). Tento problém odstraňují tzv. kombinované
lineárně-kongruentní generátory, které nepoužívají ke generování pouze jedno
předchozí číslo. Výsledek je tvořen součtem dvou pomocných náhodných čísel.
Perioda posloupnosti odpovídá
, může být na dnešních počítačích vyčerpána za
několik sekund. Aritmetika s dvojtou šířkou, pak může být neúnosně pomalá.
Další nevýhodou se později ukázala skutečnost, že skupiny generovaných čísel
vykazují geometrický vzorec, který odhaluje test na prostorové rozložení
(scatter plot test). Tento problém odstraňují tzv. kombinované
lineárně-kongruentní generátory, které nepoužívají ke generování pouze jedno
předchozí číslo. Výsledek je tvořen součtem dvou pomocných náhodných čísel.
Perioda posloupnosti odpovídá 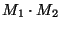 .
.
Na podobném principu jsou založeny také zpožděné (lagged) Fibonacciho
generátory. Mají však tu výhodu, že náhodné číslo závisí na některém jiném
čísle ze stejné posloupnosti a nikoliv na číslech ze dvou pomocných
posloupností. Zvyšuje se tím délka periody a snižuje míra korelací mezi prvky
posloupnosti.
kde 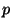 a
a 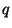 jsou zpoždění (lags), nabývající nezáporných hodnot do velikosti
posloupnosti a
jsou zpoždění (lags), nabývající nezáporných hodnot do velikosti
posloupnosti a 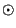 je aritmetická operace (jako +,
je aritmetická operace (jako +, 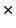 , XOR).
Výhodou je, že volbou zpoždění měníme také periodu generovaných čísel.
Nicméně je třeba připomenout, že ne vždy je složitý generátor lepší než
jednoduchý. Pokud se řeší praktické problémy (například z oblasti simulací),
pak často nezbývá nic jiného, než vyzkoušet více generátorů a zvolit ten
nejvhodnější11.
Vidíme, že klasické generátory náhodných čísel mají svoje omezení jak v délce
periody, tak v podobě nejrůznějších (často nezjistitelných) korelací mezi
čísly. Pokud se podíváme na problém filozofičtěji, pak máme pocit, že je snad
jen neschopností počítačů generovat náhodná čísla. A tak nás může napadnout,
zda není člověk schopen generovat náhodná čísla. V experimentu D.W.Hagelbargera
popsaném Claudem Shannonem, byla zvolená osoba požádána, aby vygenerovala
náhodnou posloupnost symbolů
, XOR).
Výhodou je, že volbou zpoždění měníme také periodu generovaných čísel.
Nicméně je třeba připomenout, že ne vždy je složitý generátor lepší než
jednoduchý. Pokud se řeší praktické problémy (například z oblasti simulací),
pak často nezbývá nic jiného, než vyzkoušet více generátorů a zvolit ten
nejvhodnější11.
Vidíme, že klasické generátory náhodných čísel mají svoje omezení jak v délce
periody, tak v podobě nejrůznějších (často nezjistitelných) korelací mezi
čísly. Pokud se podíváme na problém filozofičtěji, pak máme pocit, že je snad
jen neschopností počítačů generovat náhodná čísla. A tak nás může napadnout,
zda není člověk schopen generovat náhodná čísla. V experimentu D.W.Hagelbargera
popsaném Claudem Shannonem, byla zvolená osoba požádána, aby vygenerovala
náhodnou posloupnost symbolů 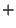 a
a  , kterou analyzoval počítač. Ten se pak na
základě rozboru této posloupnosti snažil dopředu uhodnout, jaký následující
symbol si osoba vybere. Počítač byl v předpovídání úspěšný na 55-60%, což
znamená, že ani člověk nevolí odpovědi úplně nezávisle. Jak potom ale můžeme
připravit okamžik skutečné náhody? Odpověď zní: kvantově-mechanicky.
Jedině.
Zcela přirozeně k tomu můžeme použít základní vlastnost přírody - chvíli
náhodného kolapsu vlnové funkce v jeden z vlastních stavů kvantového systému
v momentě měření. Pojďme si tedy přiblížit poměrně jednoduchý algoritmus,
kterým může kvantový počítač generovat skutečná náhodná čísla. Pokud budeme
uvažovat fyzikální systém představující qubit ve stavu
, kterou analyzoval počítač. Ten se pak na
základě rozboru této posloupnosti snažil dopředu uhodnout, jaký následující
symbol si osoba vybere. Počítač byl v předpovídání úspěšný na 55-60%, což
znamená, že ani člověk nevolí odpovědi úplně nezávisle. Jak potom ale můžeme
připravit okamžik skutečné náhody? Odpověď zní: kvantově-mechanicky.
Jedině.
Zcela přirozeně k tomu můžeme použít základní vlastnost přírody - chvíli
náhodného kolapsu vlnové funkce v jeden z vlastních stavů kvantového systému
v momentě měření. Pojďme si tedy přiblížit poměrně jednoduchý algoritmus,
kterým může kvantový počítač generovat skutečná náhodná čísla. Pokud budeme
uvažovat fyzikální systém představující qubit ve stavu 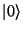 , pak úkolem
bude jej připravit do vyvážené superpozice stavů
, pak úkolem
bude jej připravit do vyvážené superpozice stavů 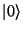 a
a 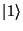 .
Toho docílíme aplikováním unitárního operátoru U s rotací
o
.
Toho docílíme aplikováním unitárního operátoru U s rotací
o 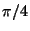 .
.
V této chvíli je systém připraven na měření. Při měření přejde systém náhodně
do jednoho z vlastních stavů této superpozice. Pokud chceme generovat vícebitová
náhodná čísla je potřeba připravit dost qubitů k reprezentaci těchto
čísel a následně vytvořit operací přímého tenzorového součinu
jeden více-qubitový registr, který poté změříme. Ukažme si tyto kroky
na jednoduchém příkladu: Řekněme, že chceme vygenerovat číslo z rozsahu
0 - 15.
- Nejprve si připravíme čtyři izolované qubity ve stavu
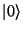 .
.
- Aplikací
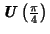 upravíme stav každého qubitu na vyváženou superpozici
upravíme stav každého qubitu na vyváženou superpozici 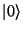 a
a 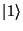 , tj.
{
, tj.
{
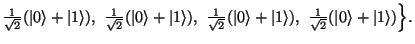
- Poté přímým součinem vytvoříme z jednotlivých qubitů jeden paměťový
registr, tj.
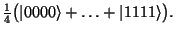
- Nakonec takto připravený registr změříme, čímž superpozice náhodně
zkolabuje do jednoho z možných stavů
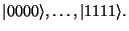
Existují tedy aplikace, které klasický počítač z principu nezvládá,
kdežto kvantový ano. Nicméně pro generování náhodných čísel se dnes už
nemusíme nutně upínat ke klasickému počítači, neboť již existují
generátory (TRNG - True Random Number Generators) využívající kvantovou
mechaniku. Dříve šlo zejména o fyzikální procesy
založené na radioaktivním rozpadu prvků. Počet těchto rozpadů detekovala
Geiger-Müllerova trubice, která výsledky následně převáděla do počítače.
Podle intervalů měření šlo generovat náhodná čísla různých rozložení.
Nevýhodou však byla většinou malá rychlost generování. Častěji se dnes proto
jako TRNG používají kvantově mechanické děje na polovodičových přechodech.
Velmi častá je detekce náhodného prvku ze šumu, který je možné naměřit
na PN přechodech polarizovaných v závěrném směru. Klasický PC tak
vlastně už dnes používá jako periferii silně degenerovaný kvantový počítač.



Next: Kvantová teleportace
Up: Kvantové algoritmy
Previous: Kvantová kryptografie
Obsah
Bashar
2001-01-23