




Next: Other universal dendrites
Up: Dendrites
Previous: Wazewski universal dendrite
Let
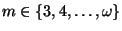 . By the
standard universal dendrite of order
. By the
standard universal dendrite of order 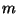 we mean a
dendrite
we mean a
dendrite 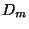 such
that each ramification point of
such
that each ramification point of 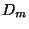 is of order
is of order 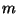 and
for each arc
and
for each arc
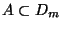 the set of ramification points
of
the set of ramification points
of 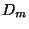 which belong to
which belong to 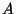 is dense in
is dense in 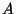 . Their
constructions, known again from [Wazewski 1923, Chapter K, p.
137] (see also [Charatonik 1991, (4), p.
168]; for the inverse limit construction
see [Chaaratonik 1980, p. 491]), mimic that of the
Wazewski universal dendrite
. Their
constructions, known again from [Wazewski 1923, Chapter K, p.
137] (see also [Charatonik 1991, (4), p.
168]; for the inverse limit construction
see [Chaaratonik 1980, p. 491]), mimic that of the
Wazewski universal dendrite 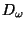 , but instead of
copies of
, but instead of
copies of 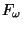 we use copies of
we use copies of 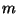 -ods at each step
of the construction.
See Figures A-C for the standard universal dendrites
-ods at each step
of the construction.
See Figures A-C for the standard universal dendrites 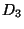 ,
,
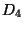 and
and 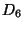 .
.
Figure 1.3.7:
( A ) standard universal dendrite 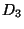
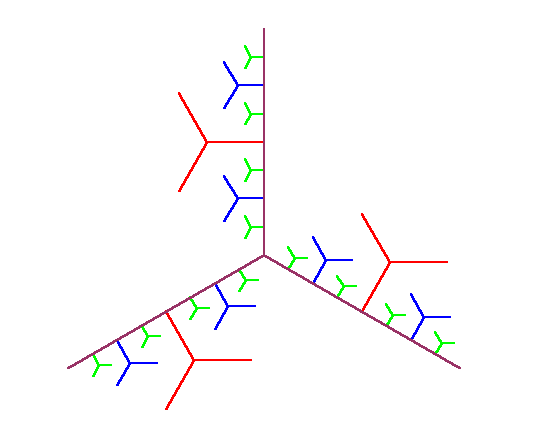 |
Figure:
( AA ) standard universal dendrite  - an animation
- an animation
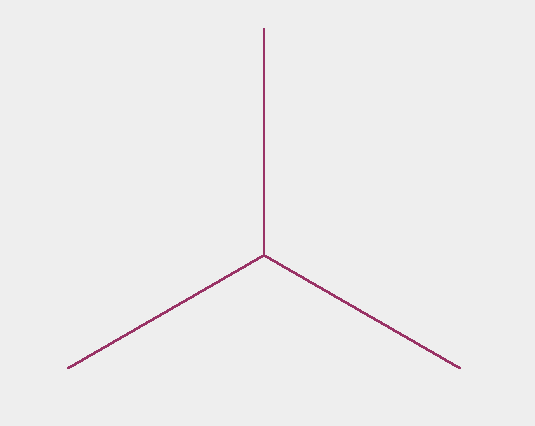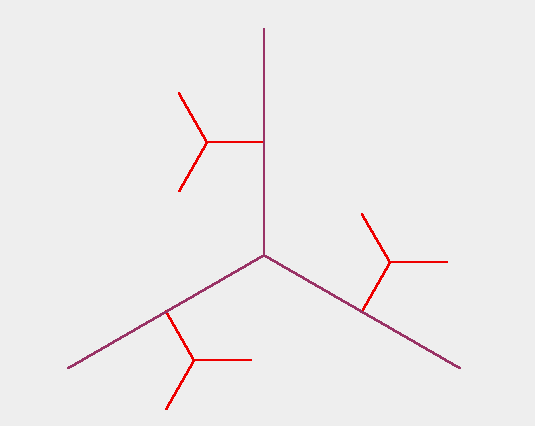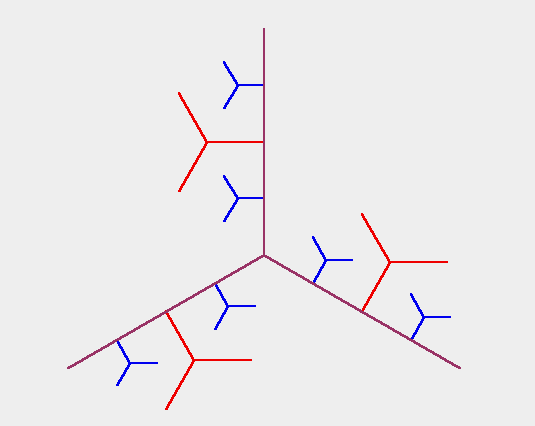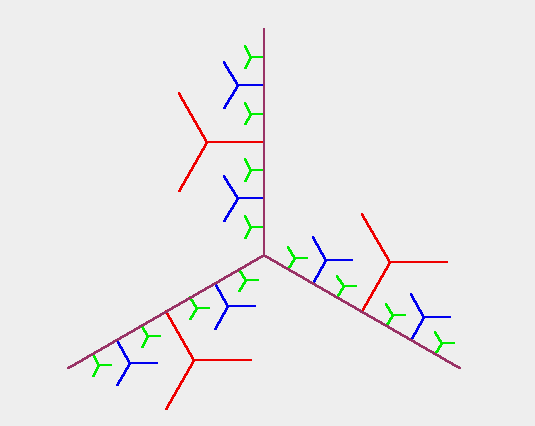 |
Figure 1.3.7:
( B ) standard universal dendrite 
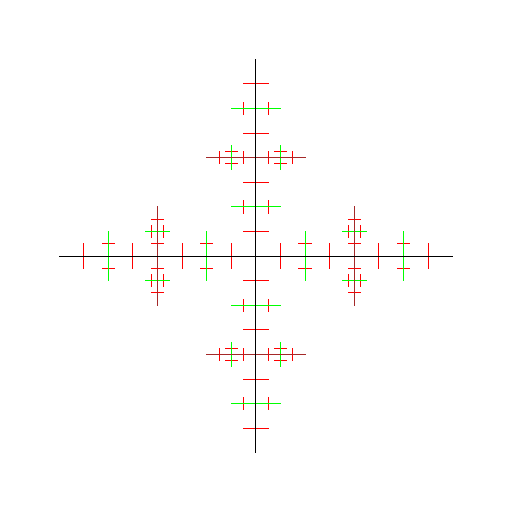 |
Figure:
( BB ) standard universal dendrite 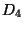 - an animation
- an animation
 |
Figure:
( BBB ) standard universal dendrite 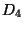 produced as an intersection - an animation
produced as an intersection - an animation
 |
Figure 1.3.7:
( C ) standard universal dendrite 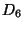
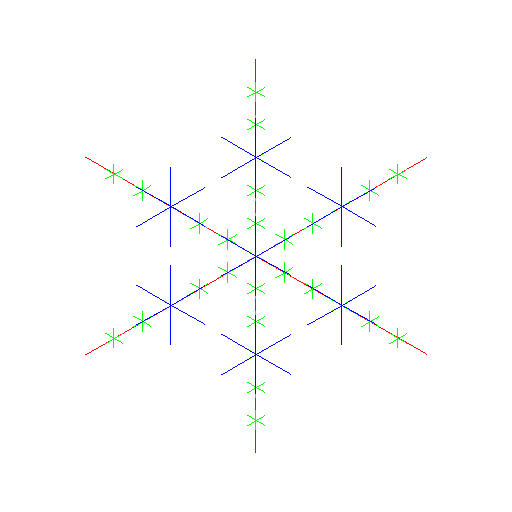 |
The standard universal dendrites 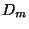 have the following properties.
have the following properties.
- For each
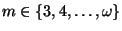
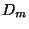 is universal in the class of all
dendrites for which the order of their ramification points
is less than or equal to
is universal in the class of all
dendrites for which the order of their ramification points
is less than or equal to 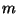 , see e.g. [Menger 1932, Chapter 10, §
6, p. 322].
, see e.g. [Menger 1932, Chapter 10, §
6, p. 322].
- If
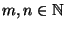 with
with
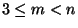 , then there exists an
open mapping of
, then there exists an
open mapping of 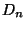 onto
onto 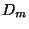 ,
[Chaaratonik 1980, Theorem 2, p. 492].
,
[Chaaratonik 1980, Theorem 2, p. 492].
- Among all standard universal dendrites
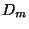 only
only 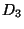 and
and
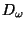 are homeomorphic with all their
open images, [Chaaratonik 1980, Corollary, p.
493].
are homeomorphic with all their
open images, [Chaaratonik 1980, Corollary, p.
493].
- For each
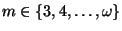 a monotone surjection of
a monotone surjection of 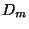 onto itself is a near
homeomorphism if and only if
onto itself is a near
homeomorphism if and only if 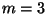 , [Charatonik 1991, Corollary 5.5,
p. 178].
, [Charatonik 1991, Corollary 5.5,
p. 178].
- Any two standard universal dendrites
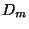 and
and
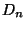 of some orders
of some orders
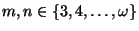 are
monotonely equivalent,
[Charatonik 1991, Corollary 6.6, p. 180].
are
monotonely equivalent,
[Charatonik 1991, Corollary 6.6, p. 180].
- For each
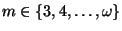 the
dendrite
the
dendrite 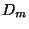 is monotonely homogeneous [Charatonik 1991, Theorem 7.1, p.
186].
is monotonely homogeneous [Charatonik 1991, Theorem 7.1, p.
186].
Other mapping properties of the standard universal dendrites 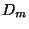 can be
found e.g. in [Chaaratonik 1980], [Charatonik 1991],
[Charatonik 1995], [Charatonik et al. 1997a], [Charatonik et al. 1998],
[Charatonik et al. 1994] and [Charatonik W.J. et al. 1994].
can be
found e.g. in [Chaaratonik 1980], [Charatonik 1991],
[Charatonik 1995], [Charatonik et al. 1997a], [Charatonik et al. 1998],
[Charatonik et al. 1994] and [Charatonik W.J. et al. 1994].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.





Next: Other universal dendrites
Up: Dendrites
Previous: Wazewski universal dendrite
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() have the following properties.
have the following properties.
![]() can be
found e.g. in [Chaaratonik 1980], [Charatonik 1991],
[Charatonik 1995], [Charatonik et al. 1997a], [Charatonik et al. 1998],
[Charatonik et al. 1994] and [Charatonik W.J. et al. 1994].
can be
found e.g. in [Chaaratonik 1980], [Charatonik 1991],
[Charatonik 1995], [Charatonik et al. 1997a], [Charatonik et al. 1998],
[Charatonik et al. 1994] and [Charatonik W.J. et al. 1994].