




Next: The dendrite
Up: Dendrites
Previous: Universal dendrites of order
For a given nonempty set
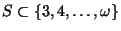 we denote by
we denote by 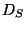 any dendrite
any dendrite  satisfying the following two conditions:
satisfying the following two conditions:
- (a)
- if
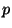 is a ramification point of
is a ramification point of  , then
, then
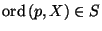 ;
;
- (b)
- for each arc
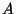 contained in
contained in  and for every
and for every 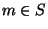 there is in
there is in 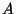 a point
a point 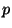 with
with
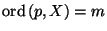 .
.
It is shown in [Charatonik W.J. et al. 1994, Theorem 6.2, p. 229]
that the
dendrite 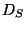 is topologically unique, i.e., if
two dendrites satisfy conditions (a) and (b) with the same
set
is topologically unique, i.e., if
two dendrites satisfy conditions (a) and (b) with the same
set
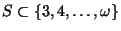 , then they are
homeomorphic. The dendrite
, then they are
homeomorphic. The dendrite 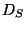 is called the
standard universal dendrite of orders in
is called the
standard universal dendrite of orders in 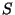 . If
. If 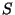 is a singleton
is a singleton 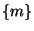 ,
then
,
then 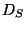 is just the
standard universal dendrite
is just the
standard universal dendrite 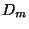 defined previously.
defined previously.
The following properties of dendrites 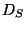 are known (see [Charatonik W.J. et al. 1994, Theorems
6.4 and 6.6-6.8, p. 230; Corollary 6.10, p. 232]).
are known (see [Charatonik W.J. et al. 1994, Theorems
6.4 and 6.6-6.8, p. 230; Corollary 6.10, p. 232]).
- For any nonempty subset
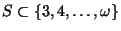 , the dendrite
, the dendrite 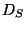 is strongly pointwise self-homeomorphic.
is strongly pointwise self-homeomorphic.
- If
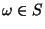 , then the dendrite
, then the dendrite 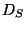 is
universal
for the family of all dendrites.
is
universal
for the family of all dendrites.
- If the set
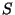 is finite with
is finite with
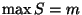 , then
, then 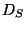 is
universal for the family of all dendrites having orders of ramification
points at most
is
universal for the family of all dendrites having orders of ramification
points at most 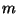 .
.
- If the set
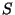 is infinite and
is infinite and
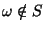 ,
then
,
then 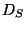 is universal for the family of all dendrites having finite orders
of ramification points.
is universal for the family of all dendrites having finite orders
of ramification points.
- Nonconstant open images of standard universal
dendrites
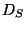 are homeomorphic to
are homeomorphic to 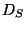 if and only if
if and only if 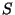 is a nonempty
subset of
is a nonempty
subset of
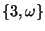 .
.
- For any nonempty subset
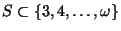 and
for an arbitrary dendrite
and
for an arbitrary dendrite 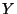 there exists a monotone mapping from
there exists a monotone mapping from 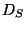 onto
onto 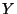 ,
[Charatonik et al. 1998, Theorem 2.22, p. 239].
,
[Charatonik et al. 1998, Theorem 2.22, p. 239].
- For any nonempty subset
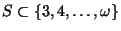 the dendrite
the dendrite 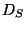 is monotonely homogeneous, [Charatonik 1996, Theorem 3.3, p. 292].
is monotonely homogeneous, [Charatonik 1996, Theorem 3.3, p. 292].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.





Next: The dendrite
Up: Dendrites
Previous: Universal dendrites of order
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() we denote by
we denote by ![]() any dendrite
any dendrite ![]() satisfying the following two conditions:
satisfying the following two conditions:
![]() are known (see [Charatonik W.J. et al. 1994, Theorems
6.4 and 6.6-6.8, p. 230; Corollary 6.10, p. 232]).
are known (see [Charatonik W.J. et al. 1994, Theorems
6.4 and 6.6-6.8, p. 230; Corollary 6.10, p. 232]).