




Next: continuum
Up: Definitions
Previous: converge 0-regularly
Given a continuum  with an arc-structure
with an arc-structure 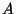 , a subset
, a subset
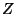 of
of  is said to be convex provided that for each pair of
points
is said to be convex provided that for each pair of
points
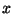 and
and 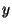 of
of 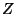 the arc
the arc 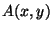 is a subset of
is a subset of 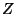 . If
. If 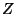 is a convex
subcontinuum of
is a convex
subcontinuum of  , then
, then
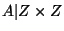 is an arc-structure on
is an arc-structure on 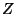 . We
define
. We
define  to be locally convex at a point
to be locally convex at a point 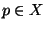 provided that
for
each open set
provided that
for
each open set 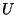 containing
containing 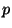 there is a convex set
there is a convex set 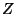 such that
such that
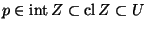 (see [Fugate et al. 1981, I.2, p. 548-549]).
(see [Fugate et al. 1981, I.2, p. 548-549]).





Next: continuum
Up: Definitions
Previous: converge 0-regularly
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30