




Next: Unicoherent continua (also hereditary)
Up: Indecomposable continua (also hereditary)
Previous: Indecomposable continua (also hereditary)
By a
Knaster continuum
is meant a
continuum homeomorphic to the inverse limit
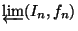 of a sequence of unit intervals
of a sequence of unit intervals
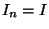 with open, non-homeomorphic bonding maps
with open, non-homeomorphic bonding maps 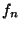 .
Denote by
.
Denote by
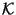 the class of all Knaster continua.
the class of all Knaster continua.
The most popular examples of Knaster continua is the
buckethandle
(sometimes called by dynamists
the
horseshoe
) 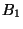 , where
, where
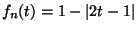 , and the
double buckethandle
, and the
double buckethandle
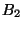 with
with
Nice geometric models of 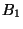 and
and 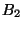 can be described
in the following way (see [Kuratowski 1968, pp. 204-205]).
If
can be described
in the following way (see [Kuratowski 1968, pp. 204-205]).
If 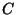 denotes the standard Cantor ternary set in
denotes the standard Cantor ternary set in 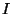 , then
, then
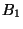 is homeomorphic to the union of all semi-circles
where
is homeomorphic to the union of all semi-circles
where
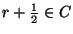 ,
and all semi-circles
for
,
and all semi-circles
for
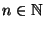 , where
, where
![r+\frac5{2\cdot3^n}\in C\cap [\frac2{3^n},\frac1{3^{n-1}}]$](img283.gif) .
.
See Figure A.
Figure 3.2.1:
( A ) buckethandle
 |
If 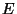 is the quintary Cantor set in
is the quintary Cantor set in 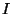 (real numbers in
(real numbers in 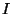 which can be written in the enumeration system at base 5 without digits 1 and 3), then
which can be written in the enumeration system at base 5 without digits 1 and 3), then
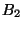 is homeomorphic to the union of all semi-circles
is homeomorphic to the union of all semi-circles
for
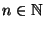 and
and
![r+\frac7{10\cdot5^n}\in E\cap
[\frac2{5^{n+1}},\frac1{5^n}]$](img286.gif) and all semi-circles
for
and all semi-circles
for 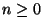 and
and
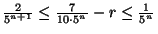 .
.
See Figure B.
Figure 3.2.1:
( B ) double buckethandle
 |
Figure:
( BB ) double buckethandle
 |
- If
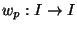 is the map such that
is the map such that
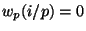 for even
for even
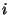 ,
,
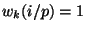 for odd
for odd 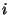 , where
, where 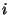 is an integer
between 0 and
is an integer
between 0 and
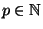 , and
, and 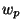 is linear on each
interval
is linear on each
interval
![[i/p,(i+1)/p]$](img295.gif) , then
, then
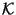 is equal to the
family of all continua homeomorphic to inverse limits
is equal to the
family of all continua homeomorphic to inverse limits
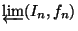 , where, for each
, where, for each 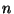 ,
, 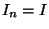 and
and
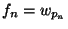 for some
for some 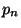 [Rogers 1970]. So, each
[Rogers 1970]. So, each
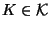 is determined by a sequence
is determined by a sequence
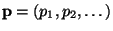 such that
such that
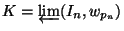 .
We will denote such
.
We will denote such 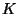 by
by
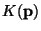 and call it a
and call it a
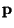 -adic Knaster continuum
. Without
loss of generality, one can assume that all
-adic Knaster continuum
. Without
loss of generality, one can assume that all 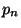 's are
prime.
's are
prime.
- Each
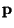 -adic Knaster continuum
-adic Knaster continuum 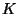 is homeomorphic
to the quotient of the
is homeomorphic
to the quotient of the
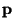 -adic
solenoid
-adic
solenoid
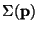 under the
relation
under the
relation
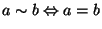
or
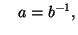
where
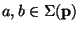 and
and 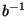 is the group
inverse of
is the group
inverse of 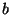 . A point of
. A point of 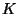 is an end point
of
is an end point
of 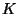 if and only if it is an image under the quotient map
of the neutral element or the element of order 2 (if such
exists) of the corresponding solenoid (see, e.g., [Krupski 1984b, p.
43]).
if and only if it is an image under the quotient map
of the neutral element or the element of order 2 (if such
exists) of the corresponding solenoid (see, e.g., [Krupski 1984b, p.
43]).
- The class
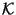 of all Knaster continua is equal to
the class of all arc-like continua with one or
two end points having the property of
Kelley and arcs as proper non-degenerate subcontinua and
which themselves are not arcs [Krupski 1984b]. In
particular, all of them are
indecomposable.
of all Knaster continua is equal to
the class of all arc-like continua with one or
two end points having the property of
Kelley and arcs as proper non-degenerate subcontinua and
which themselves are not arcs [Krupski 1984b]. In
particular, all of them are
indecomposable.
- There are
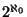 mutually non-homeomorphic members
of
mutually non-homeomorphic members
of
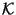 [Wa]; in fact, there is a
subfamily of
[Wa]; in fact, there is a
subfamily of
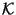 of cardinality
of cardinality
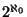 no member of which is an open image of another one [Debski 1985].
no member of which is an open image of another one [Debski 1985].
- Any open map between two Knaster continua
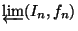 ,
,
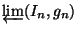 is
the uniform limit of open maps which are induced by maps
is
the uniform limit of open maps which are induced by maps
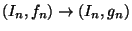 between the inverse sequences
[Eberhart et al. 1999, Theorem 4.8, p. 145].
between the inverse sequences
[Eberhart et al. 1999, Theorem 4.8, p. 145].
- If
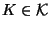 , then every indecomposable continuum
can be mapped onto
, then every indecomposable continuum
can be mapped onto 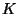 [Rogers 1970, Corollary, p. 455].
[Rogers 1970, Corollary, p. 455].
Moreover, if  is an indecomposable (Hausdorff) continuum,
is an indecomposable (Hausdorff) continuum,
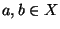 and
and 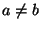 (
(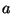 and
and 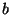 belong to different
composants of
belong to different
composants of  ), then there is a continuous
surjection
), then there is a continuous
surjection
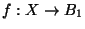 such that
such that
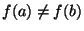 (
(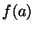 and
and 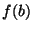 belong to different composants of
belong to different composants of 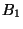 , resp.).
It follows that any indecomposable continuum embeds in the
Cartesian product of copies of
, resp.).
It follows that any indecomposable continuum embeds in the
Cartesian product of copies of 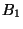 [Bellamy 1973, Corollaries 1 and
2, p. 305].
[Bellamy 1973, Corollaries 1 and
2, p. 305].
- If
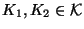 then there are
then there are
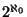 distinct homotopy types of maps of
distinct homotopy types of maps of 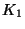 onto
onto 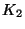 that map an end point of
that map an end point of 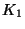 onto an end point
of
onto an end point
of 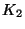 [Minc 1999].
[Minc 1999].
- If
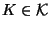 and
and 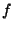 is a monotone
map of
is a monotone
map of 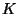 , then
, then 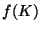 is homeomorphic to
is homeomorphic to 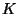 [Krupski 1984b].
[Krupski 1984b].
- There is no exactly 2-to-1 map defined on a Knaster continuum [Debski 1992].
- Knaster continua are absolute retracts
for the class of all hereditarily
unicoherent continua, i.e., if
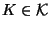 ,
,  is a
hereditarily unicoherent continuum and
is a
hereditarily unicoherent continuum and
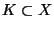 , then
, then
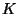 is a retract of
is a retract of  . Equivalently, if
. Equivalently, if 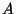 is a closed
subset of a hereditarily unicoherent continuum
is a closed
subset of a hereditarily unicoherent continuum  , then
every map
, then
every map 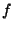 from
from 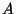 onto a Knaster continuum can be
extended over
onto a Knaster continuum can be
extended over  ([Mackowiak 1984] for
([Mackowiak 1984] for 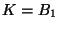 and
and  a Hausdorff hereditarily unicoherent continuum and
[Charatonik et al. XXXXa] for arbitrary
a Hausdorff hereditarily unicoherent continuum and
[Charatonik et al. XXXXa] for arbitrary
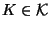 ).
).
- Any two points of a plane continuum
 can be joined by a
hereditarily decomposable
subcontinuum if and only if
can be joined by a
hereditarily decomposable
subcontinuum if and only if  cannot be mapped onto
cannot be mapped onto 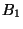 [Hagopian 1974, Theorem 2, p. 133].
[Hagopian 1974, Theorem 2, p. 133].
- Every autohomeomorphism of the buckethandle
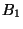 is
isotopic to some iterate of the shift
homeomorphism
is
isotopic to some iterate of the shift
homeomorphism
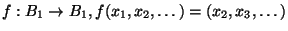 [Aarts et al. 1991, Theorem 4.4, p.
204].
[Aarts et al. 1991, Theorem 4.4, p.
204].
Moreover, any autohomeomorphism 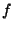 of a Knaster continuum
of a Knaster continuum
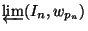 is isotopic to a standard
homeomorphism
is isotopic to a standard
homeomorphism 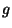 (defined as a map induced by a map
(defined as a map induced by a map
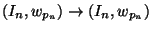 of inverse systems); maps
of inverse systems); maps
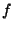 and
and 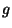 have the same topological entropy and if the
entropy is positive, then they are
semi-conjugate [Kwapisz 2001, Theorem 4, p.
271].
have the same topological entropy and if the
entropy is positive, then they are
semi-conjugate [Kwapisz 2001, Theorem 4, p.
271].
- If
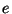 is the end point of
is the end point of 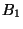 and
and 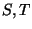 are composants
of
are composants
of 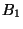 which do not contain
which do not contain 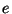 , then there exists a
continuous injection
, then there exists a
continuous injection
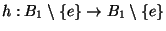 such that
such that 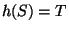 [Aarts et al. 1991, Theorem
5.1].
[Aarts et al. 1991, Theorem
5.1].
Any two composants of 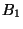 which do not contain
which do not contain 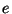 are homeomorphic [Bandt 1994].
are homeomorphic [Bandt 1994].
- Every autohomeomorphism of the buckethandle continuum has at
least two fixed points [Aarts et al. 1998].
- If
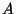 is a Borel subset of
is a Borel subset of
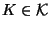 and
and 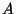 is the
union of a family of composants of
is the
union of a family of composants of 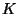 , then
, then 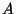 is
meager or comeager [Emeryk 1980],
[Krasinkiewicz 1974a].
is
meager or comeager [Emeryk 1980],
[Krasinkiewicz 1974a].
- Each composant
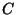 of
of 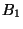 different from the
one containing the end point is internal, i.e.,
every continuum
different from the
one containing the end point is internal, i.e.,
every continuum
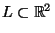 intersecting
both
intersecting
both 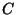 and
and
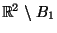 must intersect
all composants of
must intersect
all composants of 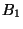 [Krasinkiewicz 1974b, Theorem, p. 261].
[Krasinkiewicz 1974b, Theorem, p. 261].
- Any Knaster continuum
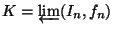 , where
, where
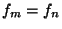 for each
for each 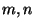 , is homeomorphic to the
attracting set of a homeomorphism
, is homeomorphic to the
attracting set of a homeomorphism
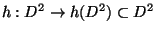 of the plane closed disk
[Barge 1986]. If
of the plane closed disk
[Barge 1986]. If
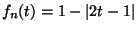 for all
for all  (i.e.,
(i.e.,
 ), then
), then 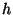 can be defined as a diffeomorphism which
is called a horse-shoe map--it was first
described by S. Smale in [Smale 1965] (see also
[Barge 1988]).
See Figure C.
can be defined as a diffeomorphism which
is called a horse-shoe map--it was first
described by S. Smale in [Smale 1965] (see also
[Barge 1988]).
See Figure C.
Figure 3.2.1:
( C ) the horse-shoe map 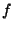 maps the stadium shaped region
maps the stadium shaped region 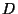 (
(
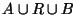 ) in such a way, that it shrinks
) in such a way, that it shrinks 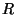 vertically,
stretches
vertically,
stretches 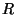 horizontally, contracts the semicircles then
folds the space once and places this result into itself so that
horizontally, contracts the semicircles then
folds the space once and places this result into itself so that
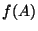 and
and 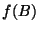 are in the interior of
are in the interior of 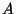 and
and  is in the interior of
is in the interior of
 .
.
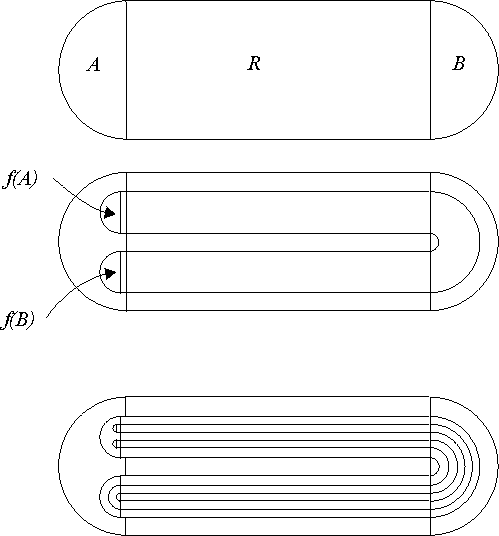 |
- The buckethandle
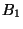 and all Knaster continua with two end
points admit no mean [Illanes XXXX],
[Kawamura et al. 1996, Theorem 2.2, p. 99].
and all Knaster continua with two end
points admit no mean [Illanes XXXX],
[Kawamura et al. 1996, Theorem 2.2, p. 99].
- The hyperspace
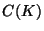 of all subcontinua of
any Knaster continuum
of all subcontinua of
any Knaster continuum 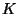 is homeomorphic to the
cone
is homeomorphic to the
cone 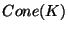 over
over 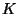 by a homeomorphism
by a homeomorphism
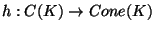 which sends
which sends 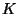 onto the vertex of
onto the vertex of
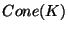 and the set of all singletons of
and the set of all singletons of 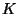 onto the base
of the cone [Dilks et al. 1981, Corollary 12, p. 639].
onto the base
of the cone [Dilks et al. 1981, Corollary 12, p. 639].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.





Next: Unicoherent continua (also hereditary)
Up: Indecomposable continua (also hereditary)
Previous: Indecomposable continua (also hereditary)
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() of a sequence of unit intervals
of a sequence of unit intervals
![]() with open, non-homeomorphic bonding maps
with open, non-homeomorphic bonding maps ![]() .
Denote by
.
Denote by
![]() the class of all Knaster continua.
the class of all Knaster continua.
![]() , where
, where
![]() , and the
double buckethandle
, and the
double buckethandle
![]() with
with
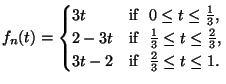
![]() is the quintary Cantor set in
is the quintary Cantor set in ![]() (real numbers in
(real numbers in ![]() which can be written in the enumeration system at base 5 without digits 1 and 3), then
which can be written in the enumeration system at base 5 without digits 1 and 3), then
![]() is homeomorphic to the union of all semi-circles
is homeomorphic to the union of all semi-circles
![]() is an indecomposable (Hausdorff) continuum,
is an indecomposable (Hausdorff) continuum,
![]() and
and ![]() (
(![]() and
and ![]() belong to different
composants of
belong to different
composants of ![]() ), then there is a continuous
surjection
), then there is a continuous
surjection
![]() such that
such that
![]() (
(![]() and
and ![]() belong to different composants of
belong to different composants of ![]() , resp.).
It follows that any indecomposable continuum embeds in the
Cartesian product of copies of
, resp.).
It follows that any indecomposable continuum embeds in the
Cartesian product of copies of ![]() [Bellamy 1973, Corollaries 1 and
2, p. 305].
[Bellamy 1973, Corollaries 1 and
2, p. 305].
![]() of a Knaster continuum
of a Knaster continuum
![]() is isotopic to a standard
homeomorphism
is isotopic to a standard
homeomorphism ![]() (defined as a map induced by a map
(defined as a map induced by a map
![]() of inverse systems); maps
of inverse systems); maps
![]() and
and ![]() have the same topological entropy and if the
entropy is positive, then they are
semi-conjugate [Kwapisz 2001, Theorem 4, p.
271].
have the same topological entropy and if the
entropy is positive, then they are
semi-conjugate [Kwapisz 2001, Theorem 4, p.
271].
![]() which do not contain
which do not contain ![]() are homeomorphic [Bandt 1994].
are homeomorphic [Bandt 1994].
