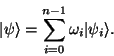


Next: Měření kvantového systému
Up: Stručný přehled kvantové mechaniky
Previous: Základní matematický aparát
Obsah
Kvantový stav představuje v kvantové mechanice reprezentaci fyzikální reality.
Ta má podle Kodaňské interpretace kvantové mechaniky dvě hlavní části. První
je část klasického světa, která odpovídá tomu, jak se na tento svět díváme a
jaký jej registrujeme. Druhou součástí je kvantový svět, který není přímo
přístupný. Můžeme z něj však pomocí aktu měření extrahovat určité informace.
V klasické části nabývá při měření kvantový systém (například energetická
hladina elektronu v atomu vodíku nebo spin elektronu) pouze diskrétní
hodnoty odpovídající skokům v celkové energii daného systému.
Na kvantové úrovni (v kvantové části světa) však mohou sledované veličiny
nabývat nekonečně mnoho hodnot odpovídajících nekonečně mnoho kvantovým stavům.
Již z těchto poznatků vidíme, že existuje zásadní rozdíl mezi systémem,
na němž bylo provedeno měření a takovým, který je izolován od okolí
a spojitě se vyvíjí. Spojitý a deterministický vývoj kvantového systému
v kvantové mechanice popisuje Schrödingerova vlnová rovnice, jejímž řešením
je vlnová funkce odpovídající danému kvantovému systému. Kvantový systém
se však může skládat z více vlnových funkcí, o kterých říkáme, že
jsou v superpozici. To znamená, že kvantový stav je vyjádřen jako
součet několika vlnových funkcí. Aby bylo zřejmé jakým příspěvkem se podílí
každá vlnová funkce na celkovém stavu, přísluší každému stavu komplexní
hodnota tzv. amplitudy pravděpodobnosti.
Z klasického pohledu nás však zajímá, jak můžeme z takového kvantového systému
získat určitou informaci. V této chvíli se dostáváme k otázce měření podrobněji.
Měření většinou provádíme tak, že vyšleme foton ke zkoumanému systému.
Foton v podobě změny své energie unáší ze systému informaci, kterou zpětně
detekujeme. Taková interakce fotonu s kvantovým systémem má však za následek
tzv. kolaps (redukci) vlnové funkce, která stochasticky přejde do
jednoho z možných stavů složeného systému. Každému stavu přísluší
výše zmíněná amplituda pravděpodobnosti. Druhá mocnina její absolutní hodnoty
udává, s jakou pravděpodobností bude změřen každý z možných stavů.
Amplituda pravděpodobnosti může být na rozdíl od klasické pravděpodobnosti
také komplexní (a záporná) a dovoluje nám tak čistě kvantovými interakcemi
(takovými, které nepředstavují přímé měření) ovlivňovat výsledek měření.
Protože měření nemusí vždy vracet numerický výsledek (např. polarizace fotonů -
horizontální  vertikální), označuje se měřitelná vlastnost fyzikálního systému jako
pozorovatelná veličina (observable). Všimněme si, že zavedením
amplitud pravděpodobností je charakter kvantového měření pravděpodobnostní,
což poukazuje na náhodný element, tvořící základ pozorovaným fyzikálním
procesům.
Nyní se zaměřme na to, jak jsou tyto poznatky kvantové mechaniky použitelné v
oblasti kvantové informatiky. U klasických počítačů jsme zvyklí
reprezentovat bit napěťovými úrovněmi, které dostatečně odlišují 0 od 1.
U kvantových počítačů je možné použít některý z dvoustavových kvantových systémů
jako je například spin částice (tj. spin 1/2 u leptonů). Takový systém může
klasicky nabývat pouze 2 hodnot (stavů):
vertikální), označuje se měřitelná vlastnost fyzikálního systému jako
pozorovatelná veličina (observable). Všimněme si, že zavedením
amplitud pravděpodobností je charakter kvantového měření pravděpodobnostní,
což poukazuje na náhodný element, tvořící základ pozorovaným fyzikálním
procesům.
Nyní se zaměřme na to, jak jsou tyto poznatky kvantové mechaniky použitelné v
oblasti kvantové informatiky. U klasických počítačů jsme zvyklí
reprezentovat bit napěťovými úrovněmi, které dostatečně odlišují 0 od 1.
U kvantových počítačů je možné použít některý z dvoustavových kvantových systémů
jako je například spin částice (tj. spin 1/2 u leptonů). Takový systém může
klasicky nabývat pouze 2 hodnot (stavů):
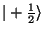 a
a
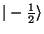 . Tak si lze představit, že bity 0 a 1 zakódujeme pomocí
jednoho a druhého spinového stavu. Spin částice je jen jeden z více možných
dvoustavových kvantových systémů, které lze použít. Jiné systémy by obstály
stejně dobře. Kvantový stav popisujeme vektorem v komplexním lineárním
Hilbertově prostoru. Každému prvku báze tohoto prostoru (tj. dimenzi) přísluší
jeden vlastní stav, do kterého může kvantový systém při měření přejít. Vlastní
stavy jsou přitom vzájemně ortogonální4. Nicméně kvantový systém
prochází podle Schrödingerovy vlnové rovnice spojitým vývojem stavového
vektoru a může tak nabývat nekonečného množství stavů. Libovolný stav
(a tím i bod Hilbertova prostoru) můžeme vyjádřit jako součet vlastních
stavů (bázových vektorů) násobených komplexními váhovými koeficienty, které
představují příspěvek daného bázového vektoru v celkovém stavu.
O takovém systému říkáme, že je v koherentní superpozici více stavů
vyjádřené jako lineární kombinace bázových vektorů.
Pro nejjednodušší případ, kdy chceme vyjádřit kvantový bit jako hodnoty
0 a 1, potřebujeme dva vlastní stavy dvojrozměrného Hilbertova prostoru.
Pak takový systém zapisujeme jako:
. Tak si lze představit, že bity 0 a 1 zakódujeme pomocí
jednoho a druhého spinového stavu. Spin částice je jen jeden z více možných
dvoustavových kvantových systémů, které lze použít. Jiné systémy by obstály
stejně dobře. Kvantový stav popisujeme vektorem v komplexním lineárním
Hilbertově prostoru. Každému prvku báze tohoto prostoru (tj. dimenzi) přísluší
jeden vlastní stav, do kterého může kvantový systém při měření přejít. Vlastní
stavy jsou přitom vzájemně ortogonální4. Nicméně kvantový systém
prochází podle Schrödingerovy vlnové rovnice spojitým vývojem stavového
vektoru a může tak nabývat nekonečného množství stavů. Libovolný stav
(a tím i bod Hilbertova prostoru) můžeme vyjádřit jako součet vlastních
stavů (bázových vektorů) násobených komplexními váhovými koeficienty, které
představují příspěvek daného bázového vektoru v celkovém stavu.
O takovém systému říkáme, že je v koherentní superpozici více stavů
vyjádřené jako lineární kombinace bázových vektorů.
Pro nejjednodušší případ, kdy chceme vyjádřit kvantový bit jako hodnoty
0 a 1, potřebujeme dva vlastní stavy dvojrozměrného Hilbertova prostoru.
Pak takový systém zapisujeme jako:
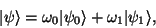
kde
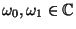 . Tyto koeficienty odpovídají
amplitudám pravděpodobnosti a mají fyzikální význam ve své druhé mocnině
absolutní hodnoty, která říká s jakou pravděpodobností naměříme příslušný
vlastní stav. Přitom součet pravděpodobností je obecně přes
. Tyto koeficienty odpovídají
amplitudám pravděpodobnosti a mají fyzikální význam ve své druhé mocnině
absolutní hodnoty, která říká s jakou pravděpodobností naměříme příslušný
vlastní stav. Přitom součet pravděpodobností je obecně přes 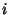 různých
vlastních stavů prostoru
různých
vlastních stavů prostoru 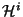 v případě, že jsou koeficienty
normovány, roven 1:
v případě, že jsou koeficienty
normovány, roven 1:
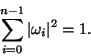
Vlastní stavy
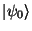 a
a
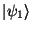 (odpovídající klasickým
bitům) se obvykle označují jako stavy
(odpovídající klasickým
bitům) se obvykle označují jako stavy 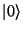 a
a 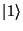 .
Pokud tyto vlastní stavy odpovídají bázovým vektorům
.
Pokud tyto vlastní stavy odpovídají bázovým vektorům
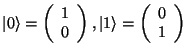 můžeme psát, že
můžeme psát, že
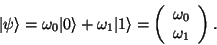
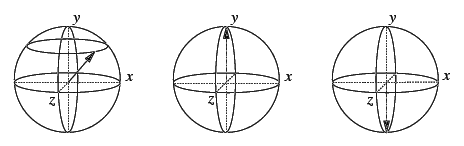
Obrázek:
Reprezentace dvoustavového systému: na obrázku vlevo je znázorněn doposud neměřený stav qubitu, v němž jsou v určitém poměru zastoupeny stavy 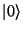 a a 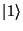 , na prostředním obrázku je pak vlastní stav , na prostředním obrázku je pak vlastní stav 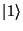 a vpravo stav a vpravo stav 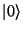 . .
|
|
Takový dvoustavový systém, který představuje kvantový bit, nebo-li
qubit, je možné názorně zobrazit jako vektor v Riemannově kouli s
umístěním v počátku souřadnic (viz obrázek). V něm je 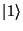 reprezentována jako vektor směřující k severnímu pólu,
reprezentována jako vektor směřující k severnímu pólu, 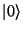 k jižnímu.
Z úhlu, který vektor
svírá se svislou osou je možné vyčíst poměrné zastoupení
k jižnímu.
Z úhlu, který vektor
svírá se svislou osou je možné vyčíst poměrné zastoupení 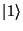 a
a
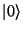 ve stavovém vektoru. Úhel, o který je vektor otočen kolem svislé
osy se nazývá fáze, která nemění poměr
ve stavovém vektoru. Úhel, o který je vektor otočen kolem svislé
osy se nazývá fáze, která nemění poměr 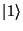 a
a 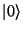 ,
ale je významná vzhledem k jevu kvantové interference, o kterém se
zmíníme později. Qubit je možné znázornit i v polárních souřadnicích
na tzv. Blochově kouli, ve které je stav qubitu vyjádřen pro úhly
polárních souřadnic
,
ale je významná vzhledem k jevu kvantové interference, o kterém se
zmíníme později. Qubit je možné znázornit i v polárních souřadnicích
na tzv. Blochově kouli, ve které je stav qubitu vyjádřen pro úhly
polárních souřadnic 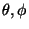 jako
jako
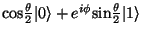 .
Pro vícestavový kvantový systém je možné výše uvedený výraz pro superpozici
zobecnit na
.
Pro vícestavový kvantový systém je možné výše uvedený výraz pro superpozici
zobecnit na
Na závěr této části si pro přehlednost shrňme, jak korespondují pojmy
kvantové mechaniky s pojmy kvantové informatiky pro qubit (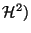 .
.
| kvantová mechanika |
kvantová informatika |
vlnová funkce 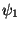 |
vlastní stav 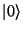 |
vlastní hodnota 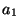 |
logická hodnota 0 |
vlnová funkce 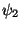 |
vlastní stav 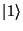 |
vlastní hodnota 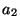 |
logická hodnota 1 |
superpozice
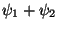 |
superpozice
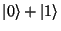 |
|



Next: Měření kvantového systému
Up: Stručný přehled kvantové mechaniky
Previous: Základní matematický aparát
Obsah
Bashar
2001-01-23
![]() vertikální), označuje se měřitelná vlastnost fyzikálního systému jako
pozorovatelná veličina (observable). Všimněme si, že zavedením
amplitud pravděpodobností je charakter kvantového měření pravděpodobnostní,
což poukazuje na náhodný element, tvořící základ pozorovaným fyzikálním
procesům.
Nyní se zaměřme na to, jak jsou tyto poznatky kvantové mechaniky použitelné v
oblasti kvantové informatiky. U klasických počítačů jsme zvyklí
reprezentovat bit napěťovými úrovněmi, které dostatečně odlišují 0 od 1.
U kvantových počítačů je možné použít některý z dvoustavových kvantových systémů
jako je například spin částice (tj. spin 1/2 u leptonů). Takový systém může
klasicky nabývat pouze 2 hodnot (stavů):
vertikální), označuje se měřitelná vlastnost fyzikálního systému jako
pozorovatelná veličina (observable). Všimněme si, že zavedením
amplitud pravděpodobností je charakter kvantového měření pravděpodobnostní,
což poukazuje na náhodný element, tvořící základ pozorovaným fyzikálním
procesům.
Nyní se zaměřme na to, jak jsou tyto poznatky kvantové mechaniky použitelné v
oblasti kvantové informatiky. U klasických počítačů jsme zvyklí
reprezentovat bit napěťovými úrovněmi, které dostatečně odlišují 0 od 1.
U kvantových počítačů je možné použít některý z dvoustavových kvantových systémů
jako je například spin částice (tj. spin 1/2 u leptonů). Takový systém může
klasicky nabývat pouze 2 hodnot (stavů):
![]() a
a
![]() . Tak si lze představit, že bity 0 a 1 zakódujeme pomocí
jednoho a druhého spinového stavu. Spin částice je jen jeden z více možných
dvoustavových kvantových systémů, které lze použít. Jiné systémy by obstály
stejně dobře. Kvantový stav popisujeme vektorem v komplexním lineárním
Hilbertově prostoru. Každému prvku báze tohoto prostoru (tj. dimenzi) přísluší
jeden vlastní stav, do kterého může kvantový systém při měření přejít. Vlastní
stavy jsou přitom vzájemně ortogonální4. Nicméně kvantový systém
prochází podle Schrödingerovy vlnové rovnice spojitým vývojem stavového
vektoru a může tak nabývat nekonečného množství stavů. Libovolný stav
(a tím i bod Hilbertova prostoru) můžeme vyjádřit jako součet vlastních
stavů (bázových vektorů) násobených komplexními váhovými koeficienty, které
představují příspěvek daného bázového vektoru v celkovém stavu.
O takovém systému říkáme, že je v koherentní superpozici více stavů
vyjádřené jako lineární kombinace bázových vektorů.
Pro nejjednodušší případ, kdy chceme vyjádřit kvantový bit jako hodnoty
0 a 1, potřebujeme dva vlastní stavy dvojrozměrného Hilbertova prostoru.
Pak takový systém zapisujeme jako:
. Tak si lze představit, že bity 0 a 1 zakódujeme pomocí
jednoho a druhého spinového stavu. Spin částice je jen jeden z více možných
dvoustavových kvantových systémů, které lze použít. Jiné systémy by obstály
stejně dobře. Kvantový stav popisujeme vektorem v komplexním lineárním
Hilbertově prostoru. Každému prvku báze tohoto prostoru (tj. dimenzi) přísluší
jeden vlastní stav, do kterého může kvantový systém při měření přejít. Vlastní
stavy jsou přitom vzájemně ortogonální4. Nicméně kvantový systém
prochází podle Schrödingerovy vlnové rovnice spojitým vývojem stavového
vektoru a může tak nabývat nekonečného množství stavů. Libovolný stav
(a tím i bod Hilbertova prostoru) můžeme vyjádřit jako součet vlastních
stavů (bázových vektorů) násobených komplexními váhovými koeficienty, které
představují příspěvek daného bázového vektoru v celkovém stavu.
O takovém systému říkáme, že je v koherentní superpozici více stavů
vyjádřené jako lineární kombinace bázových vektorů.
Pro nejjednodušší případ, kdy chceme vyjádřit kvantový bit jako hodnoty
0 a 1, potřebujeme dva vlastní stavy dvojrozměrného Hilbertova prostoru.
Pak takový systém zapisujeme jako:
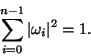
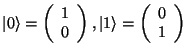 můžeme psát, že
můžeme psát, že