Stejně jako u planimetrie, i zde předpokládáme, že student má alespoň základní znalosti středoškolské stereometrie. Na následujících příkladech, které jsou posbírány většinou z přijímacích zkoušek na MFF, si můžete ověřit, zda jsou vaše znalosti dostatečné, v opačném případě doporučuji ke studiu učebnici stereometrie pro gymnázia [5].
V následujícím odstavci je uveden stručný seznam probíraných témat a k vybraným tématům je doplněn učební text.
Sylabus - stereometrie
Volné rovnoběžné promítání. Vzájemné polohy přímek a rovin v prostoru. Definice a kritéria rovnoběžnosti přímky a roviny, rovnoběžnosti dvou rovin, kolmosti přímky a roviny, kolmosti dvou rovin. Odchylka dvou přímek, odchylka dvou rovin, příčka mimoběžek (vedená daným bodem, rovnoběžná s daným směrem, nejkratší příčka). Názvosloví a vlastnosti geometrických útvarů a těles (např. hranolová plocha x hranolový prostor x hranol (specielně pak krychle, kvádr, rovnoběžnostěn)...). Eulerova věta, pravidelné mnohostěny. Řezy těles.
Volné rovnoběžné promítání
Stereometrie se zabývá studiem prostorových útvarů a jejich vzájemných vztahů. Abychom mohli s těmito prostorovými útvary účelně pracovat, a to nejen s modely, či ve svých představách, ale především v sešitě či na monitoru počítače, potřebujeme znát nějaké vhodné promítání, pomocí něhož zobrazíme trojrozměrný prostor do roviny. Pro svou jednoduchost se při řešení základních stereometrických úloh volí tzv. volné rovnoběžné promítání (dále jen VRP). Toto promítání je určeno rovinou, do které promítáme, tzv. průmětnou (π) a směrem promítání (s), který není rovnoběžný se zvolenou průmětnou. Pozor - takto zadané promítání není vzájemně jednoznačné, jelikož všechny body ležící na přímce směru promítání se zobrazí do jednoho bodu. Nelze tedy zpětně zrekonstruovat promítaný objekt.
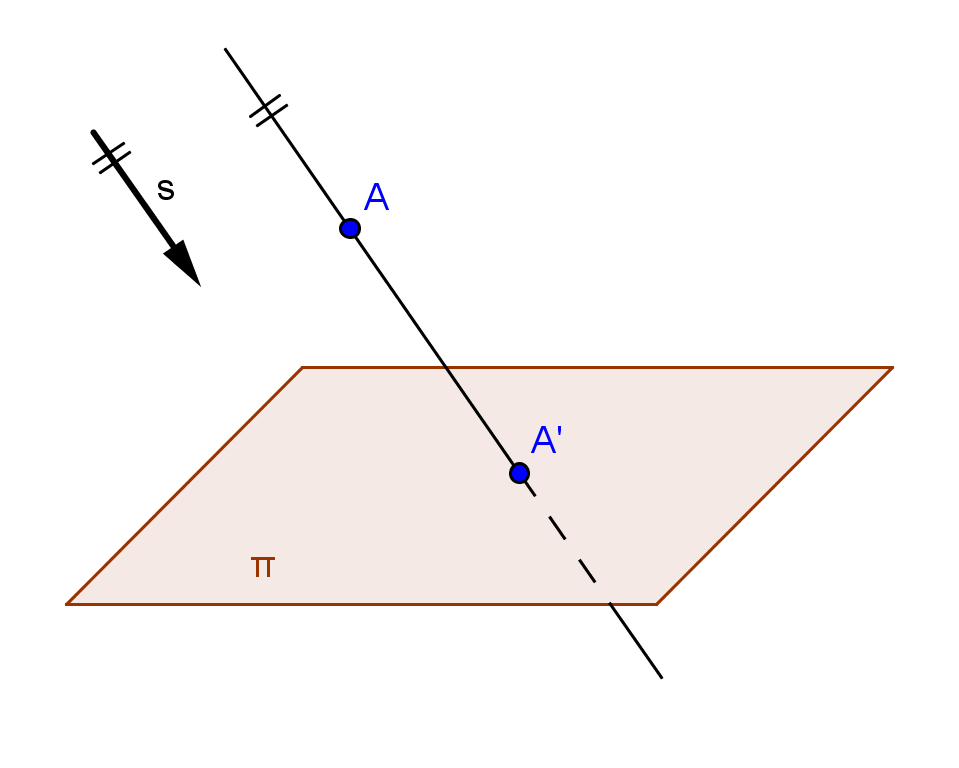π - průmětna
s - směr promítání
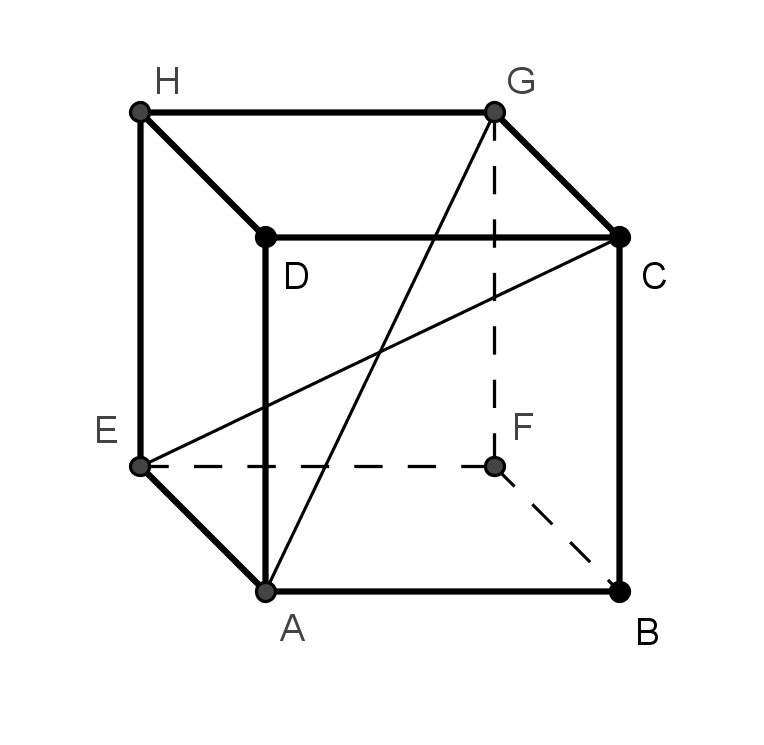
Přímka procházející bodem A ve směru promítání, je tzv. promítací přímka bodu A - protíná průmětnu v bodě A'. A' je rovnoběžným průmětem bodu A do průmětny. Body ležící v průmětně splývají se svými obrazy.
Několik základních vlastností rovnoběžného promítání:
1) Průmětem bodu je opět bod.
2) Průmětem přímky je přímka nebo bod, je-li přímka promítací (tj. směru promítání).
3) Průmětem roviny je celá průmětna, nebo jen přímka, je-li rovina promítací.
4) Rovnoběžné promítání zachovává incidenci.
5) Rovnoběžné promítání zachovává dělicí poměr.
6) Rovnoběžným průmětem dvou různých rovnoběžných přímek jsou opět rovnoběžné přímky (různé nebo splývající) nebo dva různé body, jsou-li přímky promítací.
7) Shodné a navzájem rovnoběžné úsečky se promítají do úseček, které jsou také shodné a navzájem rovnoběžné (jejich nositelky mohou splývat), nebo se promítají do dvou bodů (které mohou také splývat).
8) Útvar, který leží v průmětně, nebo v rovině s průmětnou rovnoběžné (tzv. průčelné rovině), se promítá do útvaru, který je s ním shodný.
Tělesa ve VRP zpravidla zobrazujeme tak, aby jejich podstava ležela ve vodorovné rovině (uvažujeme svislou průmětnu) a u hranatých těles volíme jednu hranu nebo stěnu v průčelné rovině. Úsečky kolmé k průmětně se zobrazí do úseček, které s obrazem vodorovných úseček svírají úhel α a jejich velikost se zkrátí, popř. prodlouží v závislosti na parametru q. Ukažme si postup nanásledujícím příkladu:
Příklad 1: Ve volném rovnoběžném promítání (α = 45°, q = 1/2) zobrazte pravidelný čtyřboký jehlan ABCDV, jehož podstavná hrana má délku 4 cm a výška měří 5 cm.
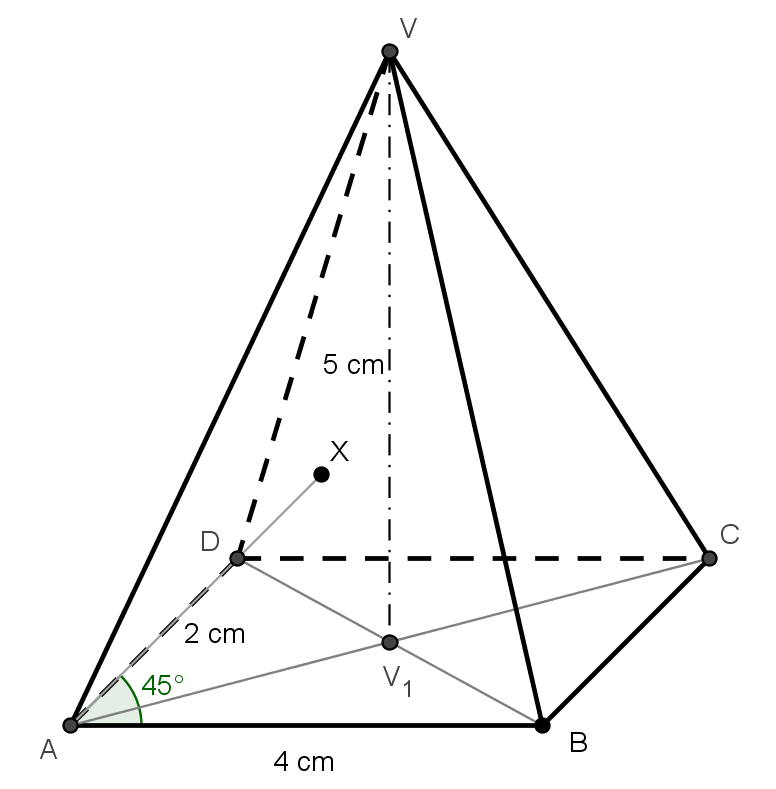1) AB, |AB| = 4cm - Zvolíme takovou polohu jehlanu, při níž podstava leží ve vodorovné rovině a hrana AB leží v průčelné rovině. Je tedy rovnoběžná s průmětnou a zobrazí se ve skutečné velikosti.
2) X, |∠BAX| = 45° - Úsečky AD a BC jsou k průmětně kolmé. Sestrojíme tedy pomocnou přímku AX, která svírá s přímkou AB úhel 45° (takové přímky jsou dvě, volbou druhé možnosti bychom dostali pouze jiný pohled na totéž těleso, viz následující applet).
3) D, |AD| = 2 cm - Na této přímce sestrojíme bod D tak, aby |AD| = |AB|/2 (opět jsou dvě možnosti volby bodu D).
4) C - Obrazem čtvercové podstavy jehlanu je rovnoběžník ABCD.
5) V1 - Dále sestrojíme patu V1 výšky jehlanu jako průsečík úhlopříček podstavy.
6) V, VV1 ⊥ AB ∧ |VV1| = 5 cm - Výška jehlanu je rovnoběžná s průmětnou a zobrazí se tedy ve skutečné velikosti, jako úsečka kolmá na úsečku AB.
7) ABCDV - Při rýsování hran jehlanu nesmíme zapomenout na jejich viditelnost!
V následujícím appletu je na obrazu krychle ukázáno, jaký vliv mají na výsledný průmět parametry α a q. Velikost těchto parametrů můžete měnit na posuvnících v pravé části appletu. Při změně velikosti úhlu α si všímejte i pojmenování jednotlivých pohledů na krychli. Pro účel vytvoření appletu je zde trochu netradičně úhel α volen jako orientovaný úhel, jehož velikost je možno zvolit v rozpětí 0° až 360°, zatímco většinou je tento úhel popisován pouze jako neorientovaný úhel (tj. např. úhel 135° (225°, 315°) v appletu je totéž jako 45°, pro rozlišení těchto úhlů se požívá pojmenování pohledů - levý nadhled, pravý nadhled, ...)
|
Zde si můžete applet stáhnout do svého počítače. |
Nejčastěji se v učebnicích setkáme s tělesy zobrazenými v pravém nadhledu, parametry VRP se volí 45° a 1/2. Ne vždy je však tato volba nejvhodnější, jak je vidět z následujících obrázků, na nichž je zobrazena krychle ABCDEFGH a dvě její tělesové úhlopříčky AG a EC (levý obrázek - pravý nadhled, 45°, 1/2; obrázek uprostřed - pravý nadhled, 60°, 1/2; pravý obrázek - levý nadhled, 45°, 1/2). Při volbě parametrů VRP je tedy třeba dbát na to, aby vzniklý obrázek byl jasný a srozumitelný. V technické praxi je zvykem zobrazovat tělesa v nadhledu, z podhledu se zobrazují pouze některé stavební prvky (římsy, balkony, klenby).
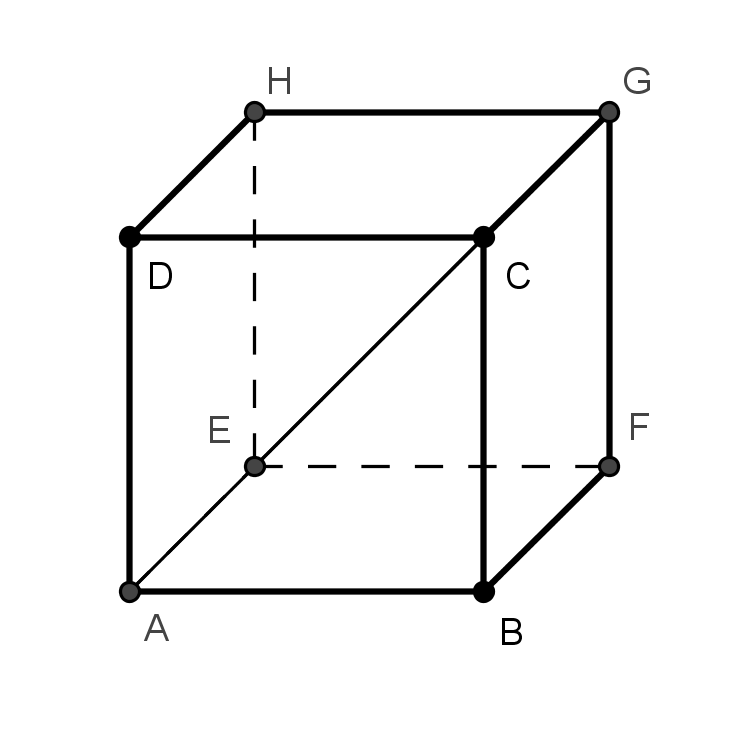
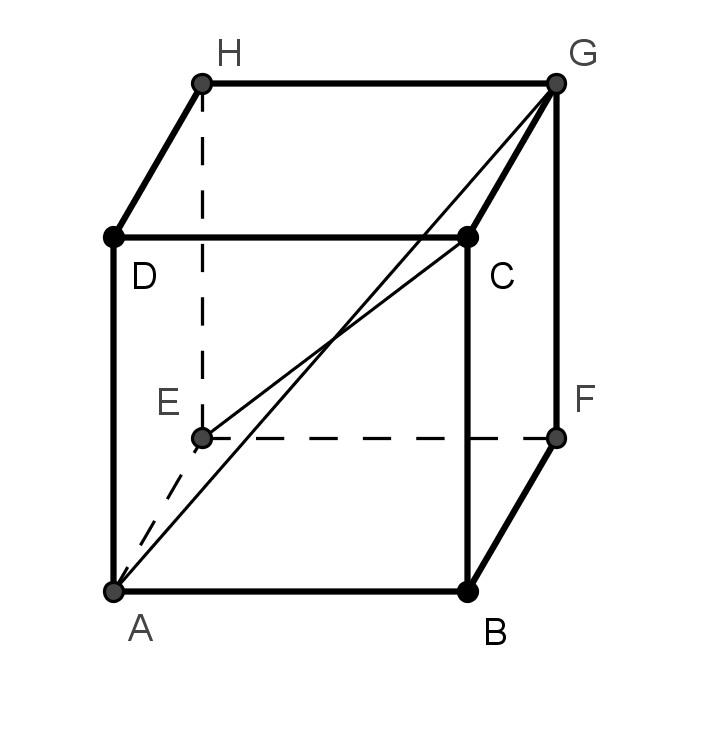
Zde najdete několik úloh na procvičení různých pohledů na krychli (PDF).
V následujících příkladech nezapomeňte na viditelnost jednotlivých hran zobrazovaných těles.
Příklad 2: Ve volném rovnoběžném promítání (pravý nadhled, 45°, 1/2) sestrojte rovnostranný trojúhelník ve vodorovné rovině, jehož strana má délku 5 cm.
Příklad 3: Ve volném rovnoběžném promítání a) (levý nadhled, 45°, 1/2) b) (pravý nadhled, 60°; 3/4) sestrojte krychli ABCDEFGH o hraně délky 5 cm.
Příklad 4: Ve volném rovnoběžném promítání (pravý podhled, 60°; 3/4) sestrojte pravidelný šestiboký jehlan ABCDEFV, jestliže podstavná hrana má délku 4 cm a výška jehlanu měří 6 cm.
Příklad 5: Ve volném rovnoběžném promítání (pravý nadhled, 45°, 1/2) sestrojte pravidelný pětiboký jehlan ABCDEV, jehož podstava je vepsána do kružnice o poloměru 6 cm a výška měří 5 cm.
Příklad 6: Ve volném rovnoběžném promítání (pravý nadhled, 60°, 1/2) sestrojte pravidelný pětiboký jehlan ABCDEV, jehož podstavná hrana má délku 3,5 cm a výška měří 6 cm. Nápověda - str. 26 [3]
Řezy hranatých těles
Pod pojmem řez tělesa rovinou budeme rozumět hledání průniku tělesa a roviny. Průnikem je rovinný útvar, u něhož nás v tuto chvíli zajímá především jeho hranice, později se budeme věnovat i jeho tvaru. Hranice řezu je lomená čára, která leží na povrchu tělesa a její vrcholy leží na hranách tělesa. Sestrojit řez tedy znamená sestrojit průsečnice jednotlivých stěn s rovinou řezu.
Při konstrukci řezu hranatého tělesa rovinou je třeba znát následující tři věty (částečně převzato z [6], str. 61):
1) Leží-li dva různé body v rovině, pak přímka jimi určená leží v téže rovině.
2) Dvě rovnoběžné roviny jsou proťaty třetí rovinou, která s nimi není rovnoběžná, ve dvou rovnoběžných přímkách.
3) Tři roviny, z nichž žádné dvě nejsou rovnoběžné a žádná není rovnoběžná s průsečnicí zbývajících dvou, mají společný právě jeden bod.
Z těchto vět vyplývají tři užitečné důsledky ([5], str. 39):
1) Leží-li dva různé body roviny řezu v téže stěně tělesa, leží v rovině této stěny i jejich spojnice. Průnik spojnice a stěny je jednou stranou řezu.
2) Jsou-li roviny dvou stěn rovnoběžné a přitom různoběžné s rovinou řezu, jsou průsečnice roviny řezu s rovinami těchto stěn rovnoběžné.
3) Průsečnice rovin dvou sousedních stěn (tj. stěn se společnou hranou) s rovinou řezu a přímka, v níž leží společná hrana, se protínají v jednom bodě.
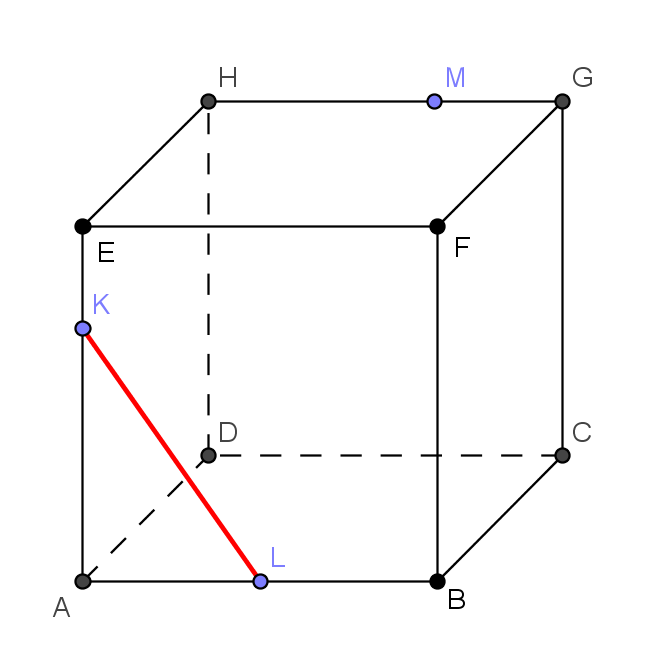
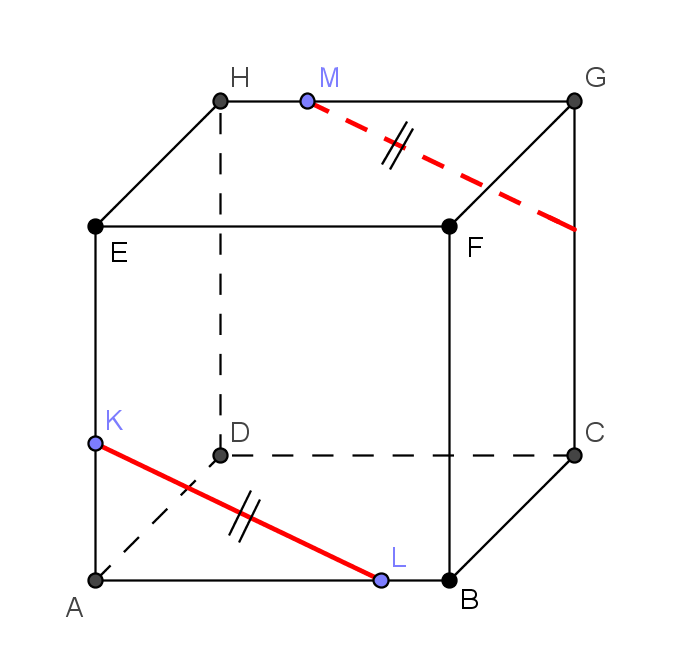
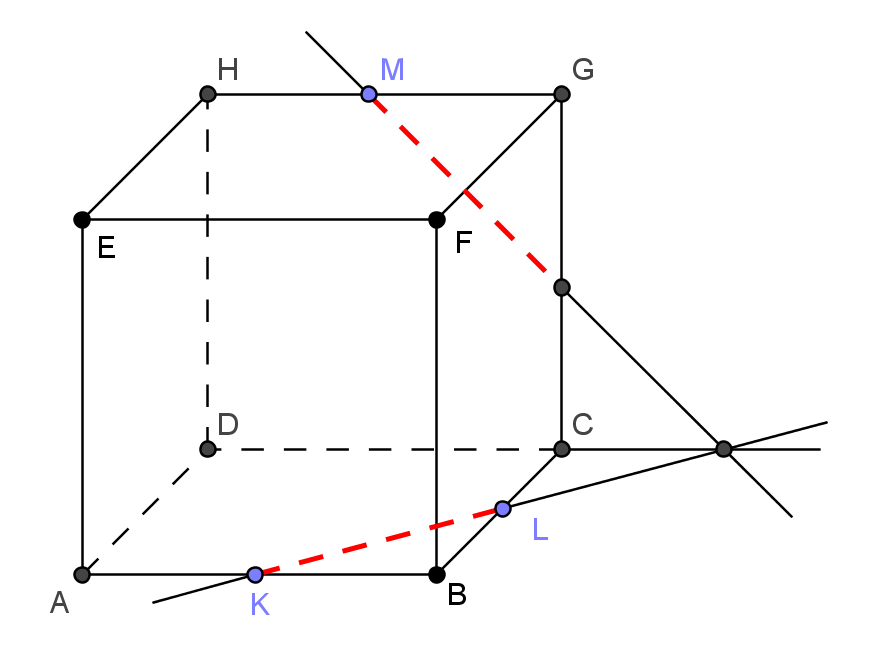
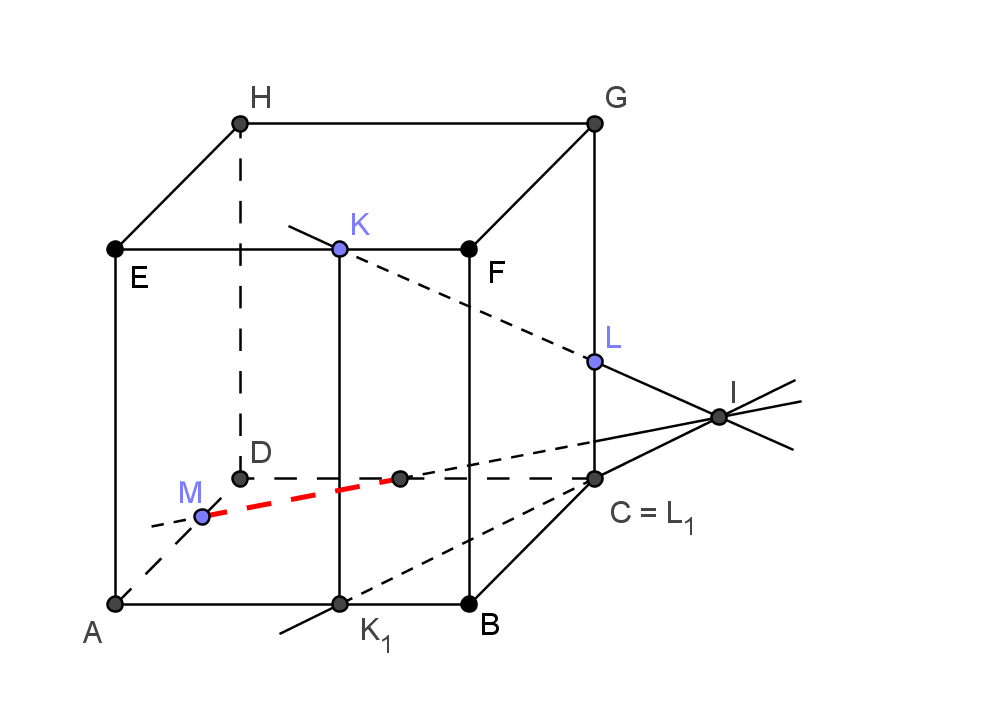Rovina řezu může být zadána i třemi body, znichž žádné dva neleží v téže stěně tělesa. Pak je třeba použít větu č. 3 v trochu jiné podobě, než je důsledek č. 3. Za tři roviny, které mají právě jeden společný bod, můžeme považovat také rovinu řezu, rovinu podstavy ABCD a rovinu kolmou k podstavné rovině procházející přímkou KL (viz. obrázek vpravo). Jinými slovy zkonstruujeme průsečík přímky KL s rovinou, v níž leží třetí zadaný bod roviny řezu M, v tomto případě např. s podstavnou rovinou ABCD (mohli bychom též zvolit stěnu ADHE). Využijeme k tomu pomocnou rovinu, která je kolmá k podstavě ABCD, v obecném případě rovnoběžná s pobočnými hranami, je-li řezaným tělesem hranol (kolmý i kosý), popř. procházející hlavním vrcholem, jeli řezaným tělesem jehlan. Na průsečnici pomocné roviny s podstavou (zde je to přímka K1L1) leží i hledaný průsečík (bod I) přímky KL s podstavnou rovinou ABCD. Tím získáme dva body roviny řezu v téže stěně tělesa a na jejich spojnici již leží část řezu. Další části řezu již získáme s využitím výše uvedených důsledků 1) - 3).
Zde najdete několik příkladů na řezy těles (PDF)