




Next: 2-dimensional locally connected continua
Up: Cyclic examples of locally
Previous: Sierpinski carpet
The
Menger universal curve
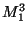 is the subset of the unit cube
is the subset of the unit cube 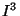 whose
projections onto faces of the cube are the
Sierpinski carpets, i.e.,
whose
projections onto faces of the cube are the
Sierpinski carpets, i.e.,
[Menger 1926].
Other descriptions can be found in 1.4.1
(see also [Mayer et al. 1986, pp. 5-6, 8-9]).
See Figure A.
Figure 1.4.3:
( A ) Menger universal curve
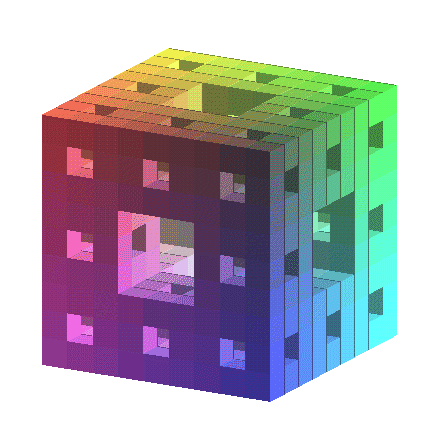 |
Figure:
( AA ) Menger universal curve - an animation
 |
- The following statements are equivalent:
 is homeomorphic to
is homeomorphic to 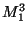 ;
;
 is a locally connected curve with no local cut points
and no planar open nonempty subsets [Anderson 1958, Theorem XII, p. 13];
is a locally connected curve with no local cut points
and no planar open nonempty subsets [Anderson 1958, Theorem XII, p. 13];
 is a homogeneous locally connected curve
different from a simple close curve [Anderson 1958, Theorem XIII, p.
14];
is a homogeneous locally connected curve
different from a simple close curve [Anderson 1958, Theorem XIII, p.
14];
 is a locally connected curve with the disjoint arcs property (see
Property 3 in 1.4.1);
is a locally connected curve with the disjoint arcs property (see
Property 3 in 1.4.1);
 is a locally connected curve and each arc in
is a locally connected curve and each arc in  is
approximately non-locally-separating arc and has empty interior in
is
approximately non-locally-separating arc and has empty interior in  [Krupski et al. XXXXa, Theorem 3, p. 86].
[Krupski et al. XXXXa, Theorem 3, p. 86].
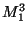 is universal in the class of all
metric separable spaces of dimension
is universal in the class of all
metric separable spaces of dimension 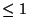 [Menger 1926].
[Menger 1926].
- Z-setsZ-set in
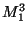 coincide with
non-locally-separating closed subsets of
coincide with
non-locally-separating closed subsets of  .
.
If 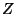 is a separable metric space of dimension
is a separable metric space of dimension 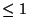 ,
then
,
then 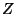 can be embedded as a non-locally-separating subset of
can be embedded as a non-locally-separating subset of 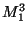 [Mayer et al. 1986, Theorem 6.1, p. 42].
[Mayer et al. 1986, Theorem 6.1, p. 42].
- If
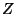 is a closed subset of a metric space
is a closed subset of a metric space  ,
,
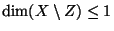 and
and
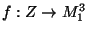 is a
continuous mapping with non-locally separating image
is a
continuous mapping with non-locally separating image  ,
then
,
then 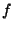 can be extended to a map
can be extended to a map
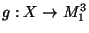 such that
such that
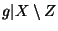 is an embedding into
is an embedding into
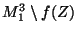 [Mayer et al. 1986, Theorem 6.4, p. 44].
[Mayer et al. 1986, Theorem 6.4, p. 44].
- Every continuous surjection
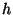 between
non-locally separating closed subsets
between
non-locally separating closed subsets 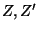 of
of 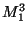 extends to a mapping
extends to a mapping 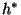 of
of 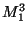 such that
such that
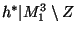 is a homeomorphism onto
is a homeomorphism onto
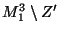 [Mayer et al. 1986, Corollary 6.5, p. 44];
moreover, for every
[Mayer et al. 1986, Corollary 6.5, p. 44];
moreover, for every
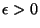 there exists
there exists 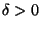 such that if
such that if 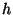 is a
is a 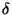 -homeomorphism,
then
-homeomorphism,
then 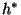 can be taken as an
can be taken as an 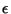 -homeomorphism
(see Property 4b in 1.4.1).
-homeomorphism
(see Property 4b in 1.4.1).
- For each locally connected continuum
 , there exist open surjections
, there exist open surjections
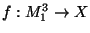 and
and
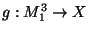 such that
such that 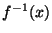 is
homeomorphic to
is
homeomorphic to 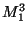 and
and 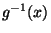 is a Cantor set,
for any
is a Cantor set,
for any 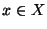 [Wilson 1972].
[Wilson 1972].
- Any compact 0-dimensional group
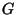 acts freely on
acts freely on 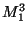 so that the orbit space
so that the orbit space 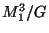 is homeomorphic to
is homeomorphic to 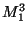 [Anderson 1957, Theorem 1].
[Anderson 1957, Theorem 1].
- If a locally compact space
 contains a topological copy
of
contains a topological copy
of 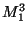 , then the space of all copies of
, then the space of all copies of 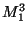 in
in  with the Hausdorff metricHausdorff metric is a true
absolute
with the Hausdorff metricHausdorff metric is a true
absolute
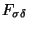 -set
[Krupski XXXXb].
-set
[Krupski XXXXb].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.





Next: 2-dimensional locally connected continua
Up: Cyclic examples of locally
Previous: Sierpinski carpet
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() is the subset of the unit cube
is the subset of the unit cube ![]() whose
projections onto faces of the cube are the
Sierpinski carpets, i.e.,
whose
projections onto faces of the cube are the
Sierpinski carpets, i.e.,
![]() is a separable metric space of dimension
is a separable metric space of dimension ![]() ,
then
,
then ![]() can be embedded as a non-locally-separating subset of
can be embedded as a non-locally-separating subset of ![]() [Mayer et al. 1986, Theorem 6.1, p. 42].
[Mayer et al. 1986, Theorem 6.1, p. 42].