




Next: Sierpinski carpet
Up: Cyclic examples of locally
Previous: Cyclic examples of locally
The Menger universal continuum
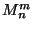 , for
, for 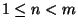 [Menger 1926], can
be defined as follows [Engelking 1978, pp. 121-122].
[Menger 1926], can
be defined as follows [Engelking 1978, pp. 121-122].
Let
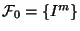 .
Inductively, suppose a collection
.
Inductively, suppose a collection
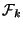 of
cubes has been defined for
of
cubes has been defined for 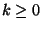 . Divide each
cube
. Divide each
cube
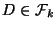 into
into
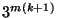 congruent cubes
with edges of length
congruent cubes
with edges of length
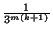 . If
. If
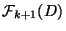 is the collection of all these
cubes that intersect
is the collection of all these
cubes that intersect 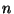 -dimensional faces of
-dimensional faces of 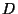 , then let
, then let
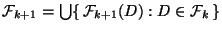 .
.
Define
The most popular continua are 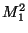 , widely known as the
Sierpinski universal plane curve or the Sierpinski
carpet [Sierpinski 1916], and
, widely known as the
Sierpinski universal plane curve or the Sierpinski
carpet [Sierpinski 1916], and
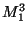 , called the
Menger universal curve
[Menger 1926]. These particular curves
are discussed separately.
, called the
Menger universal curve
[Menger 1926]. These particular curves
are discussed separately.
Continuum
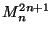 can also be obtained as the
inverse limit
can also be obtained as the
inverse limit
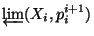 in the following way.
Let
in the following way.
Let
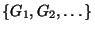 be an open base of
be an open base of 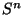 consisting of
open
consisting of
open 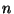 -cells such that
-cells such that
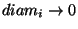 . Put
. Put 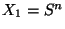 and
and
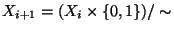 , where relation
, where relation 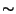 identifies points
identifies points
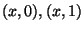 iff
iff
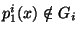 .
The bonding maps
.
The bonding maps 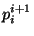 are natural retractions [Pasynkov 1965], [Bestvina 1988, pp. 98-99].
are natural retractions [Pasynkov 1965], [Bestvina 1988, pp. 98-99].
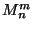 is the universal space in the
class of all compacta of dimension
is the universal space in the
class of all compacta of dimension 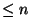 which embed in
which embed in
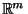 [Štanko 1971] ([Menger 1926] for
[Štanko 1971] ([Menger 1926] for
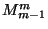 ).
). 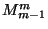 is universal in the class of all
is universal in the class of all
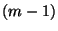 -dimensional subsets of
-dimensional subsets of
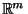 ([Engelking 1978, Problem
1.11.D]), and
([Engelking 1978, Problem
1.11.D]), and
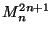 in the class of
all
in the class of
all 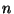 -dimensional separable metric spaces
[Bothe 1963].
-dimensional separable metric spaces
[Bothe 1963].
- A continuum
 is homeomorphic to
is homeomorphic to 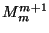 if and only
if
if and only
if  can be embedded in the
can be embedded in the 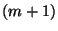 -sphere
-sphere 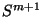 in such a way that
in such a way that
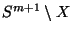 has infinitely
many components
has infinitely
many components
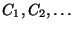 such that
such that
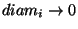 ,
,
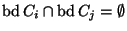 for
for  ,
,
 is an
is an
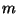 -cell for each
-cell for each 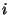 and
and
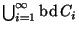 is dense in
is dense in  (see [Cannon 1973] and [Chigogidze et al. 1995, Theorem 6.1.2, p. 74]).
(see [Cannon 1973] and [Chigogidze et al. 1995, Theorem 6.1.2, p. 74]).
- A continuum
 is homeomorphic to
is homeomorphic to
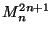 if and only
if
if and only
if  is
is 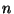 -dimensional,
-dimensional, 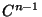 and
and
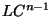 -space with the
disjoint
-space with the
disjoint 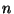 -disks property
(
-disks property
(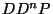 property) [Bestvina 1988, Corollary 5.2.3,
p.98].
property) [Bestvina 1988, Corollary 5.2.3,
p.98].
Equivalently,  is homeomorphic to
is homeomorphic to
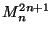 if and
only if
if and
only if  is
is 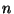 -dimensional,
-dimensional, 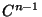 and
and
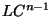 -space such that any continuous map from a compact
space of dimension
-space such that any continuous map from a compact
space of dimension 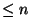 into
into
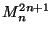 is a uniform
limit of embeddings (Z-embeddings)
[Bestvina 1988, Theorem 2.3.8, p. 36].
is a uniform
limit of embeddings (Z-embeddings)
[Bestvina 1988, Theorem 2.3.8, p. 36].
- If
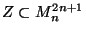 is a Z-setZ-set, then, for
every open neighborhood
is a Z-setZ-set, then, for
every open neighborhood
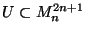 of
of 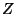 and
every
and
every
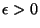 , there is
, there is 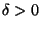 such that if
such that if
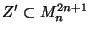 is a Z-set and
is a Z-set and 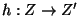 is a
is a
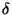 -homeomorphism, then
-homeomorphism, then 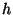 extends to an
extends to an
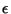 -homeomorphism
-homeomorphism
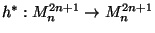 such that
such that
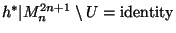 [Bestvina 1988, Theorem 3.1.1, p. 65].
[Bestvina 1988, Theorem 3.1.1, p. 65].
- For every
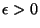 , there exists
, there exists 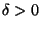 such that if
such that if 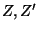 are Z-setsZ-set in
are Z-setsZ-set in
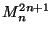 and
and 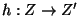 is a
is a 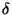 -homeomorphism,
then there is an
-homeomorphism,
then there is an 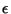 -homeomorphism
-homeomorphism
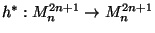 extending
extending 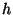 [Bestvina 1988, Theorem 3.1.3, p. 71].
[Bestvina 1988, Theorem 3.1.3, p. 71].
- Every homeomorphism between Z-sets in
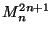 extends to an autohomeomorphism of
extends to an autohomeomorphism of
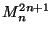 [Bestvina 1988, Corollary 3.1.5, p. 72].
[Bestvina 1988, Corollary 3.1.5, p. 72].
It follows that
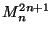 is strongly locally homogeneous and
countably dense homogeneous.
is strongly locally homogeneous and
countably dense homogeneous.
- If
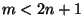 , then
, then 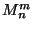 is not homogeneous
[Lewis 1987] (for
is not homogeneous
[Lewis 1987] (for 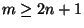 the homogeneity of
the homogeneity of 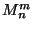 follows from the property above).
follows from the property above).
-
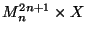 is not 2-homogeneous for an arbitrary
continuum
is not 2-homogeneous for an arbitrary
continuum  [Kuperberg et al. 1995].
[Kuperberg et al. 1995].
- The groups of autohomeomorphisms of
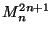 and
and
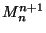 are Polish and one-dimensional
(see [Oversteegen et al. 1994, Corollary 6]
and Property 2).
are Polish and one-dimensional
(see [Oversteegen et al. 1994, Corollary 6]
and Property 2).
The group is totally disconnected for
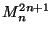 (see [Brechner 1966, Theorem 1.3] for
(see [Brechner 1966, Theorem 1.3] for  and its natural extension for any
and its natural extension for any 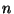 ).
).
- The Polish group of autohomeomorphisms of
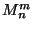 is
at most one-dimensional [Oversteegen et al. 1994].
is
at most one-dimensional [Oversteegen et al. 1994].
- The group of autohomeomorphisms of
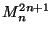 is
simple (see [Chigogidze et al. 1995, Theorem
3.2.4]).
is
simple (see [Chigogidze et al. 1995, Theorem
3.2.4]).
- Every autohomeomorphism of
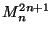 is
a composition of two homeomorphisms,
each of which is the
identity on some nonempty open set [Sakai 1994].
is
a composition of two homeomorphisms,
each of which is the
identity on some nonempty open set [Sakai 1994].
- For each
![t\in[n,2n+1]$](img236.gif) , there is a copy of
, there is a copy of
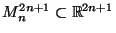 with the
Hausdorff dimension
with the
Hausdorff dimension  [Chigogidze et al. 1995, Theorem
4.2.6].
[Chigogidze et al. 1995, Theorem
4.2.6].
- Every Z-set in
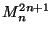 is the fixed point set of
some autohomeomorphisms of
is the fixed point set of
some autohomeomorphisms of
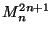 [Sakai 1997].
[Sakai 1997].
- Any
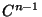 and
and 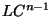 -continuum is the image of
-continuum is the image of
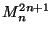 under a
under a 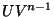 -map
[Bestvina 1988, Theorem 5.1.8, p. 95].
-map
[Bestvina 1988, Theorem 5.1.8, p. 95].
- If a Polish space
 contains a topological copy
contains a topological copy 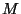 of
of
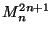 or
or 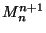 , then the space of all copies
of
, then the space of all copies
of 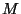 in
in  with the Hausdorff metric
is not a
with the Hausdorff metric
is not a
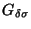 -set [Krupski XXXXb].
-set [Krupski XXXXb].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.





Next: Sierpinski carpet
Up: Cyclic examples of locally
Previous: Cyclic examples of locally
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() , for
, for ![]() [Menger 1926], can
be defined as follows [Engelking 1978, pp. 121-122].
[Menger 1926], can
be defined as follows [Engelking 1978, pp. 121-122].
![]() .
Inductively, suppose a collection
.
Inductively, suppose a collection
![]() of
cubes has been defined for
of
cubes has been defined for ![]() . Divide each
cube
. Divide each
cube
![]() into
into
![]() congruent cubes
with edges of length
congruent cubes
with edges of length
![]() . If
. If
![]() is the collection of all these
cubes that intersect
is the collection of all these
cubes that intersect ![]() -dimensional faces of
-dimensional faces of ![]() , then let
, then let
![]() .
.
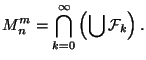
![]() , widely known as the
Sierpinski universal plane curve or the Sierpinski
carpet [Sierpinski 1916], and
, widely known as the
Sierpinski universal plane curve or the Sierpinski
carpet [Sierpinski 1916], and
![]() , called the
Menger universal curve
[Menger 1926]. These particular curves
are discussed separately.
, called the
Menger universal curve
[Menger 1926]. These particular curves
are discussed separately.
![]() can also be obtained as the
inverse limit
can also be obtained as the
inverse limit
![]() in the following way.
Let
in the following way.
Let
![]() be an open base of
be an open base of ![]() consisting of
open
consisting of
open ![]() -cells such that
-cells such that
![]() . Put
. Put ![]() and
and
![]() , where relation
, where relation ![]() identifies points
identifies points
![]() iff
iff
![]() .
The bonding maps
.
The bonding maps ![]() are natural retractions [Pasynkov 1965], [Bestvina 1988, pp. 98-99].
are natural retractions [Pasynkov 1965], [Bestvina 1988, pp. 98-99].
![]() is homeomorphic to
is homeomorphic to
![]() if and
only if
if and
only if ![]() is
is ![]() -dimensional,
-dimensional, ![]() and
and
![]() -space such that any continuous map from a compact
space of dimension
-space such that any continuous map from a compact
space of dimension ![]() into
into
![]() is a uniform
limit of embeddings (Z-embeddings)
[Bestvina 1988, Theorem 2.3.8, p. 36].
is a uniform
limit of embeddings (Z-embeddings)
[Bestvina 1988, Theorem 2.3.8, p. 36].
![]() (see [Brechner 1966, Theorem 1.3] for
(see [Brechner 1966, Theorem 1.3] for ![]() and its natural extension for any
and its natural extension for any ![]() ).
).