Definice posloupnosti
Definice
Funkce, jejímž definičním oborem \(D\) je buď množina všech přirozených čísel \(N=\{1,2,3,4,...\}\), nebo její podmnožina všech přirozených čísel \(n\) menších nebo rovno \(n_0\), kde \(n_0\) je pevně dané číslo z \(N\).
Pokud je definiční obor posloupnosti konečná množina, pak se posloupnost nazývá konečná.
Pokud je definiční obor posloupnosti nekonečná množina, pak se posloupnost nazývá nekonečná.
Značení: Je zvykem prvky z definičního oboru posloupnosti označovat \(n\) (případně \(k\), \(l\), \(i\), ...) a funkční hodnoty posloupnosti označovat \(a_{n}\) (případně \(b_{n}\), \(a_{k}\), ...) a nazývat je členy posloupnosti.
Grafem posloupnosti je množina diskrétních (izolovaných) bodů.
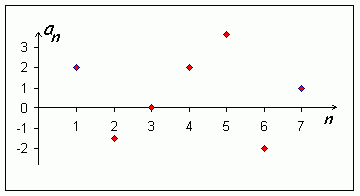
Obr. 1.1: Graf posloupnosti
