Posloupnosti a řady

Vlastnosti posloupností

Jelikož posloupnosti jsou pouze speciální typ funkce, vlastnosti a jejich definice vám jistě budou povědomé. U posloupností se ale většinou zkoumá pouze monotónnost a omezenost dané posloupnosti. Tím lépe, nebude toho tolik.

Monotónnost posloupnosti

Definice

Posloupnost $(a_n)$ se nazývá rostoucí právě tehdy, když

$\forall n, m \in D: n \lt m \Rightarrow a_n \lt a_m$

Pro zjišťování, zda je posloupnost rostoucí se nám bude více hodit následující věta. Bude řečena pouze pro nekonečnou posloupnost s definičním oborem $N$ , po drobné úpravě by ovšem platila i pro konečné posloupnosti. U konečných posloupností je třeba dát pozor na "kraje" definičního oboru.

Věta

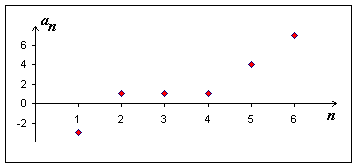
Posloupnost

$(a_n)_{n=1}^{\infty}$ je rostoucí právě tehdy, když

$\forall n \in N$ platí

$a_{n+1} \gt a_n$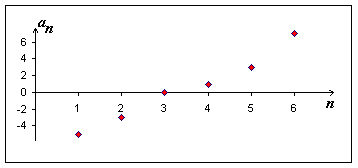

Obr. 3.1: Graf rostoucí posloupnosti

Příklady

$\{-1, 1, 3, 5, 7, \ldots \}$

$a_n = 5n^2 - 13$

$a_n = a_{n-1} + 5$ ,

$a_1 = 1$

Definice

Posloupnost $(a_n)$ se nazývá klesající právě tehdy, když

$\forall n, m \in D: n \lt m \Rightarrow a_n \gt a_m$

Věta

Posloupnost

$(a_n)_{n=1}^{\infty}$ je klesající právě tehdy, když

$\forall n \in N$ platí

$a_{n+1} \lt a_n$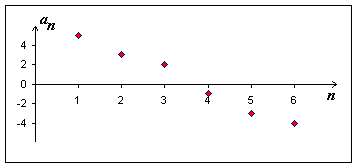

Obr. 3.2: Graf klesající posloupnosti

Příklady

$\{1, {1 \over 2}, {1 \over 3}, {1 \over 4}, {1 \over 5}, \ldots \}$

$a_n = {3 \over n^2} + 1,3$

$a_{n + 2} = 2a_{n+1} - a_n$ ,

$a_1 = 1$ ,

$a_2 = 0$

Definice

Posloupnost $(a_n)$ se nazývá nerostoucí právě tehdy, když

$\forall n, m \in D: n \lt m \Rightarrow a_n \ge a_m$

Věta

Posloupnost

$(a_n)_{n=1}^{\infty}$ je nerostoucí právě tehdy, když

$\forall n \in N$ platí

$a_{n+1} \le a_n$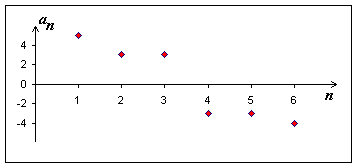

Obr. 3.3: Graf nerostoucí posloupnosti

Příklady

$\{1, 1, 1, 1, 1, \ldots \}$

$a_n = {3 \over n^2} + 1,3$

$a_{n + 1} = a_n - 3$ ,

$a_1 = 1$

Definice

Posloupnost $(a_n)$ se nazývá neklesající právě tehdy, když

$\forall n, m \in D: n \lt m \Rightarrow a_n \le a_m$

Věta

Posloupnost

$(a_n)_{n=1}^{\infty}$ je neklesající právě tehdy, když

$\forall n \in N$ platí

$a_{n+1} \ge a_n$

Obr. 3.4: Graf neklesající posloupnosti

Příklady

$\{0, 1, 1, 2, 2, 3, 3, 4, \ldots \}$

$a_n = 2^n$

$a_{n + 2} = a_{n + 1} + a_n$ ,

$a_1 = 1$ ,

$a_2 = 1$

Vlastnosti posloupností

Monotónnost posloupnosti

Titulní stránka

Úvod

Definice

Zadání

Vlastnosti

Speciální posloupnosti

Limita

Řady

Rejstřík