Příklad 4
Jsou dány různoběžné přímky \(p\), \(q\), jejich průsečík \(S\) a trojúhelník \(ABC\). Sestrojte všechny rovnoramenné trojúhelníky \(SXY\) se základnou \(XY\) takové, že výška na základnu leží na přímce \(p\), bod \(X\) leží na některé ze stran trojúhelníka \(ABC\) a bod \(Y\) leží na přímce \(q\).
Rozbor
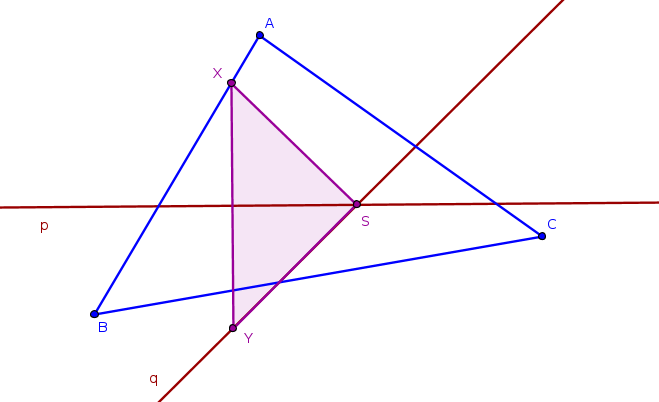
Obr. 3.2.4 - Náčrtek příkladu 4
- Trojúhelník \(SXY\) je rovnoramenný, proto přímka \(p\), na které leží výška na základnu trojúhelníka, je zároveň osou souměrnosti trojúhelníka \(SXY\).
- Bod \(Y\) leží na přímce \(q\), tedy i strana \(SY\) leží na přímce \(q\). Proto bod \(X\) leží na obrazu \(q'\) přímky \(q\) v osové souměrnosti s osou \(p\).
- Bod \(X\) získáme jako průsečík obrazu \(q'\) přímky \(q\) a strany daného trojúhelníka \(ABC\).
Konstrukce a zápis konstrukce
Applet 3.2.5 - Příklad 4
Diskuse
- Úloha nemá řešení, pokud přímka \(q'\) neprotne žádnou stranu trojúhelníka \(ABC\).
- Úloha má právě jedno řešení, pokud bod \(S\) leží na některé ze stran trojúhelníka \(ABC\) nebo pokud existuje právě jeden průsečík přímky \(q'\) a některé ze stran trojúhelníka \(ABC\) (průsečíkem je některý z vrcholů trojúhelníka).
- Úloha má právě dvě řešení pro všechna ostatní umístění přímky \(q'\) a trojúhelníka \(ABC\).
Další příklady
| Příklad 1 | Příklad 2 | Příklad 3 | Příklad 4 | Příklad 5 | Příklad 6 |
