Příklad 5
Je dána přímka \(p\), na ní bod \(Z\). Dále je dán bod \(X\) tak, že \(|XZ|=4\) cm. Zkonstruujte všechny kosodélníky \(VXYZ\) s obvodem \(14\) cm tak, aby bod \(Y\) ležel na přímce \(p\).
Rozbor
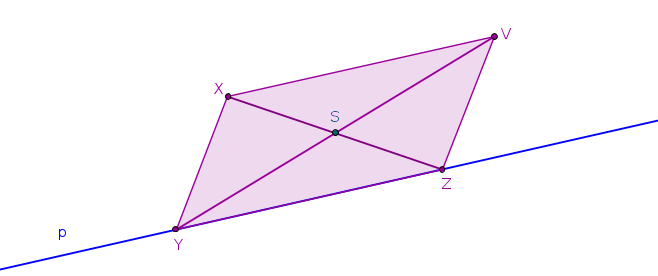
Obr. 3.2.5 - Náčrtek příkladu 5
- Úsečka \(XZ\) je úhlopříčkou kosodélníka, rozděluje kosodélník na dva shodné trojúhelníky. Konstrukci si zjednodušíme, nejprve zkonstruujeme trojúhelník \(XYZ\) a z něj pak získáme kosodélník.
- Pro trojúhelník \(XYZ\) bude platit, že součet délek stran \(XY\) a \(YZ\) bude roven polovině odvodu kosodélníka \(VXYZ\).
- Ke konstrukci trojúhelníka \(XYZ\) využijeme pomocného rovnoramenného trojúhelníka \(XRY\), podívejme se na následující obrázek.
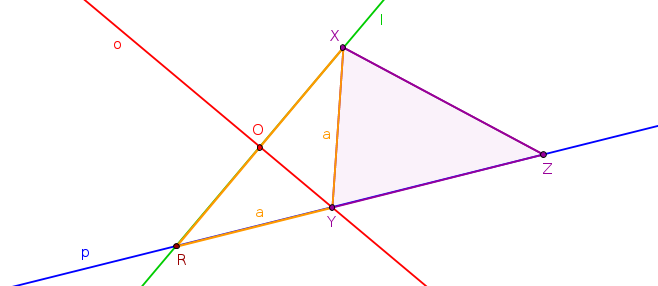
Obr. 3.2.6 - Pomocná konstrukce
- Bod \(Y\) leží na přímce \(p\), leží na ní tedy i strana \(YZ\).
- Sestrojíme trojúhelník \(XZR\) tak, aby bod \(R\) ležel na přímce \(p\) a \(|RZ|=7\) cm, tj. součtu délek stran \(XY\) a \(YZ\).
- Nyní najdeme bod \(Y\). K tomu využijeme vlastnosti rovnoramenného trojúhelníka - ramena trojúhelníka jsou stejně dlouhá (\(|XY|=|RY|\)). Proto \(|XY|+|YZ|=|RY|+|YZ|\). Rovnoramenný trojúhelník je osově souměrný podle jedné osy, přímky \(o\), na které leží výška na základnu. Takže přímka \(o\) je kolmá na úsečku \(XR\) a prochází jejím středem. Bod \(Y\) je průsečík přímky \(o\) a přímky \(p\).
- Bod \(V\) sestrojíme s využitím vlastností kosodélníka.
Konstrukce a zápis konstrukce
Applet 3.2.6 - Příklad 5
Diskuse
Počet řešení závisí na umístění bodu \(X\).
- Úloha nemá řešení, pokud bod \(X\) leží na přímce \(p\).
- Úloha má právě dvě řešení pro všechna ostatní umístění bodu \(X\).
Další příklady
| Příklad 1 | Příklad 2 | Příklad 3 | Příklad 4 | Příklad 5 | Příklad 6 |
