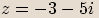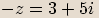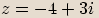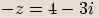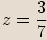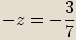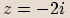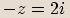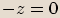Definice algebraického tvaru
Obraz komplexního čísla v algeraickém tvaru
Každé komplexní číslo  lze vyjádřit ve tvaru
lze vyjádřit ve tvaru 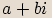 . Reálné číslo
. Reálné číslo 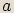 nazýváme
reálnou částí komplexního čísla, reálné číslo
nazýváme
reálnou částí komplexního čísla, reálné číslo 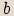 imaginární částí. Komplexní číslo
imaginární částí. Komplexní číslo 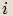 , pro něhož platí
, pro něhož platí 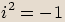 , nazýváme
imaginární jednotkou.
Výraz
, nazýváme
imaginární jednotkou.
Výraz 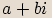 nazveme algebraickým tvarem komplexního čísla
nazveme algebraickým tvarem komplexního čísla  .
.
Poznámka
Komplexní číslo  dané v algebraickém tvaru zapisujeme
dané v algebraickém tvaru zapisujeme 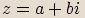 .
.
Poznámka
Každé komplexní číslo 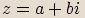 lze vyjádřít ve tvaru uspořádané dvojice
lze vyjádřít ve tvaru uspořádané dvojice
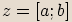 .
.
Klasifikace komplexních čísel
 , komplexní číslo
, komplexní číslo 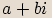 nazýváme reálné.
nazýváme reálné. 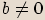 , komplexní číslo
, komplexní číslo 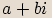 nazveme imaginární.
nazveme imaginární. 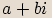 nazýváme ryze imaginární,
jestliže
nazýváme ryze imaginární,
jestliže  .
. Rovnost komplexních čísel
Definice
Dvě komplexní čísla v algebraickém tvaru se rovnají, rovnají-li se jejich reálné části a zároveň jejich imaginární části.
 Čísla
Čísla 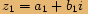 a
a 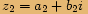 se rovnají, pokud
se rovnají, pokud  a zároveň
a zároveň  .
>>nahoru<<
.
>>nahoru<<
Absolutní hodnota komplexního čísla
Definice
Absolutní hodnota komplexního čísla
Absolutní hodnotou komplexního čísla  vyjádřeného ve tvaru
vyjádřeného ve tvaru 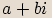 nazveme reálné číslo
nazveme reálné číslo 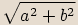 ,
značíme ji
,
značíme ji 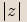 .
.
Příklady
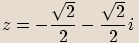
 Pokud
Pokud 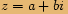 , potom
, potom 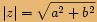 .
.
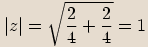

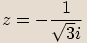
 Zlomek rozšíříme výrazem
Zlomek rozšíříme výrazem 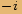 , abychom
odstranili imaginární jednotku ze jmenovatele.
, abychom
odstranili imaginární jednotku ze jmenovatele.
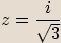
 Absolutní hodnota podílu je podíl absolutních hodnot.
Absolutní hodnota podílu je podíl absolutních hodnot.
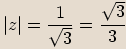



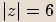

>>nahoru<<
Číslo komplexně sdružené
Definice
Komplexně sdružená čísla
Číslem komplexně sdruženým ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 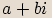 nazýváme komplexní číslo
nazýváme komplexní číslo 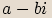 ,
značíme ho
,
značíme ho  .
.

Příklady




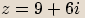

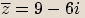





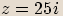



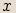 ,
, 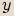 budou komplexní čísla
budou komplexní čísla 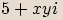 ,
,  komplexně sdružená.
komplexně sdružená. Dvě čísla jsou komplexně sdružená, pokud se jejich
Dvě čísla jsou komplexně sdružená, pokud se jejichreálné složky rovnají a imaginární složky se liší znaménkem.
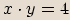
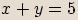

 nebo
nebo


Opačné číslo
Definice
Opačná čísla
Opačným číslem ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 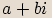 nazýváme komplexní číslo
nazýváme komplexní číslo 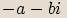 ,
značíme ho
,
značíme ho 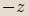 .
.

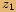 a
a 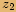 nazveme navzájem
nazveme navzájemopačná, pokud reálná část
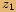 má opačné znaménko
má opačné znaménkonež reálná část
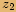 a imaginární část
a imaginární část 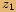
opačné znaménko než imaginární část
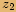 .
.
Příklady