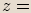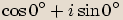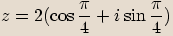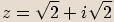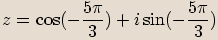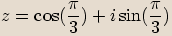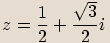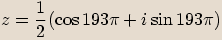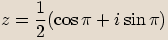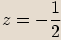Definice goniometrického tvaru
Obrazem libovolného komplexního čísla  v Gaussově rovině
je bod
v Gaussově rovině
je bod 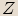 , který lze zadat pomocí kartézských
souřadnic. Za jeho
, který lze zadat pomocí kartézských
souřadnic. Za jeho 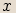 -ovou souřadnici vezmeme reálnou část
čísla
-ovou souřadnici vezmeme reálnou část
čísla  , za
, za 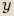 -ovou souřadnici imaginární část čísla
-ovou souřadnici imaginární část čísla  .
Tento způsob zadávání obrazů komplexních čísel se využívá pro komplexní čísla
ve tvaru uspořádaných dvojic a v algebarickém tvaru.
.
Tento způsob zadávání obrazů komplexních čísel se využívá pro komplexní čísla
ve tvaru uspořádaných dvojic a v algebarickém tvaru.
Vedle tohoto způsobu existuje ještě jiný. Obraz 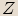 nenulového komplexního čísla
nenulového komplexního čísla  lze určit pomocí jeho vzdálenosti od počátku
lze určit pomocí jeho vzdálenosti od počátku  kartézské soustavy souřadnic a velikosti orientovaného úhlu, jehož počáteční rameno je
kladná poloosa
kartézské soustavy souřadnic a velikosti orientovaného úhlu, jehož počáteční rameno je
kladná poloosa 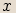 a koncové rameno polopřímka
a koncové rameno polopřímka 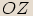 .
Tento způsob se využívá pro komplexní čísla v goniometrickém tvaru.
.
Tento způsob se využívá pro komplexní čísla v goniometrickém tvaru.
Obraz komplexního čísla  takto nelze zadat, protože bod
takto nelze zadat, protože bod 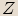 splyne s počátkem
soustavy
splyne s počátkem
soustavy  a body
a body 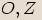 potom neurčují žádnou polopřímku, takže nelze určit velikost
orientovaného úhlu.
potom neurčují žádnou polopřímku, takže nelze určit velikost
orientovaného úhlu.
Definice
Obraz komplexního čísla v goniometrickém tvaru
Zápis nenulového komplexního čísla  ve tvaru
ve tvaru 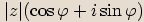 nazýváme
goniometrickým tvarem komplexního čísla
nazýváme
goniometrickým tvarem komplexního čísla  . Kladné číslo
. Kladné číslo 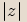 nazýváme absolutní hodnotou čísla
nazýváme absolutní hodnotou čísla  .
Reálné číslo
.
Reálné číslo  se nazývá
argument komplexního čísla
se nazývá
argument komplexního čísla  a zadávat ho lze ve stupních nebo v radiánech.
a zadávat ho lze ve stupních nebo v radiánech.
Poznámka
Komplexní číslo  dané v goniometrickém tvaru zapisujeme
dané v goniometrickém tvaru zapisujeme 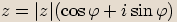 .
.
Souvislost goniometrického tvaru s algebraický tvarem
Souvislost mezi goniometrickým a algebraickým tvarem
Nechť bod 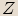 je obrazem komplexního čísla
je obrazem komplexního čísla  v Gaussově rovině.
Algebraický tvar čísla
v Gaussově rovině.
Algebraický tvar čísla  je
je 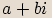 .
Protože platí, že
.
Protože platí, že
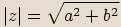 ,
, 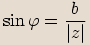 a
a 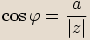 ,
,
je souvislost mezi algebraickým a goniometrickým tvarem komplexního čísla vyjádřena zápisem![]() .
.
Poznámka
Kosinus je sudá funkce, proto 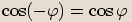 . Sinus je lichá funkce, proto
. Sinus je lichá funkce, proto 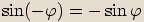 . A tedy
. A tedy 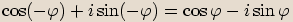 .
.
Jednoznačnost goniometrického tvaru
Protože funkce kosinus a sinus jsou periodické s periodou 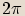 , goniometrický tvar
komplexního čísla
, goniometrický tvar
komplexního čísla  není určen jednoznačně. Je-li totiž číslo
není určen jednoznačně. Je-li totiž číslo  argumentem komplexního čísla
argumentem komplexního čísla
 , pak jím je také každé reálné číslo tvaru
, pak jím je také každé reálné číslo tvaru 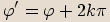 , kde
, kde 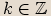 . Je-li
. Je-li 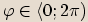 , říkáme mu
, říkáme mu
hlavní hodnota argumentu čísla a goniometrický tvar tohoto čísla je pak určen jednoznačně.
Poznámka
Budeme-li při řešení příkladů uvádět výsledky v goniometrickém tvaru, budeme argumenty převádět na jejich hlavní hodnoty.
Poznámka
Je-li  komplexní jednotka, pak goniometrický tvar tohoto čísla
je
komplexní jednotka, pak goniometrický tvar tohoto čísla
je 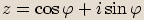 , kde
, kde  je příslušný argument.
je příslušný argument.
Řešený příklad
V goniometrickém tvaru s hlavní hodnotou argumentu zapište číslo 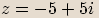 .
.
Zadané číslo chceme vyjádřit ve tvaru 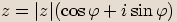 , kde
, kde 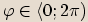 .
.
Vypočítáme absolutní hodnotu čísla: 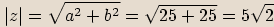
Určíme argument čísla: 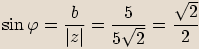 , tedy
, tedy
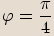 nebo
nebo 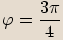
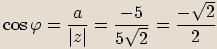 , tedy
, tedy
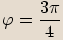 nebo
nebo 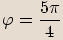
A tedy 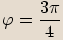 .
.
Goniometrický tvar je 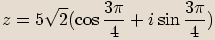 .
.
Příklad
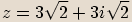 .
.
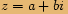 , potom
, potom 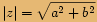 .
.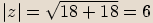

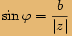
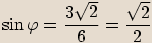

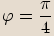 nebo
nebo 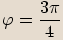

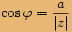
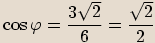

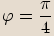 nebo
nebo 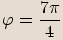
 tedy
tedy 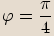

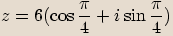

Máme-li zapsat komplexní číslo v goniometrickém tvaru, lze použít také následující postup, který bývá rychlejší.
Řešený příklad
V goniometrickém tvaru s hlavní hodnotou argumentu zapište číslo 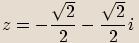 .
.
Spočítáme absolutní hodnotu čísla: 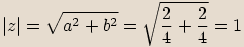
Podle znamének u jednotlivých složek čísla  určíme, ve kterém kvadrantu Gaussovy roviny obraz tohoto čísla leží.
V našem případě jsou obě znaménka záporná, takže obraz čísla leží ve třetím kvadrantu.
určíme, ve kterém kvadrantu Gaussovy roviny obraz tohoto čísla leží.
V našem případě jsou obě znaménka záporná, takže obraz čísla leží ve třetím kvadrantu.
Pokud budeme dále uvažovat komplexní číslo, jehož obě složky jsou kladné, tj. leží v prvním kvadrantu,
pro jeho argument
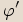 platí:
platí: 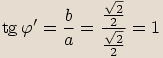 , tedy
, tedy 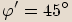
Naše číslo však leží ve třetím kvadrantu, proto ve skutečnosti 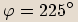 .
.
Goniometrický tvar je
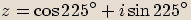 .
.
Příklady
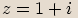

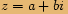 , potom
, potom 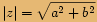 .
.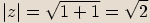

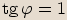

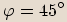
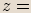

 leží v prvním kvadrantu.
leží v prvním kvadrantu.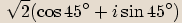



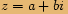 , potom
, potom 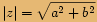 .
.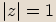
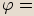

 leží v kladné části imaginární osy.
leží v kladné části imaginární osy.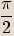
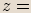

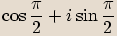

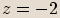

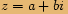 , potom
, potom 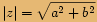 .
.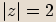
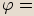

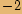 leží v záporné části reálné osy.
leží v záporné části reálné osy.
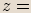

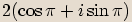

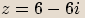

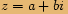 , potom
, potom 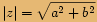 .
.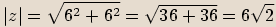

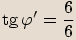

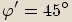
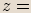

 leží ve čtvrtém kvadrantu.
leží ve čtvrtém kvadrantu.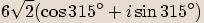

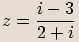

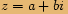 , potom
, potom 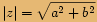 .
.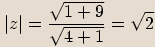
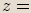

 .
.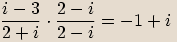

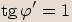

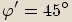
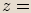

 leží ve druhém kvadrantu.
leží ve druhém kvadrantu.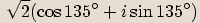

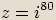

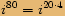
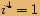

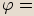

 leží v kladné části reálné osy.
leží v kladné části reálné osy.