Násobení komplexních čísel v goniometrickém tvaru
Vynásobíme-li výraz 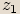 , který se rovná
, který se rovná 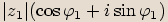 , výrazem
, výrazem 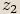 , který se rovná
, který se rovná 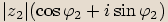 , dostáváme následující vztah
, dostáváme následující vztah
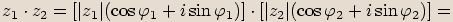
 .
.
Použijeme-li součtové vzorce pro sinus a kosinus  ,
,  ,
dostáváme
,
dostáváme
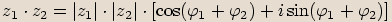 .
.
Pokud budeme oba výrazy 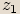 a
a 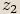 chápat jako komplexní čísla zapsaná v
goniometrickém tvaru, povede nás to k následující definici.
chápat jako komplexní čísla zapsaná v
goniometrickém tvaru, povede nás to k následující definici.
Definice
Součin dvou komplexních čísel
Máme-li dvě nenulová komplexní čísla  a
a  , pak
jejich součinem nazveme komplexní číslo
, pak
jejich součinem nazveme komplexní číslo 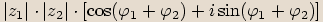 . Tento součin
značíme
. Tento součin
značíme  .
.

že vynásobíme jejich absolutní hodnoty a sečteme argumenty.
Poznámka
Pravidlo pro násobení komplexních čísel v goniometrickém tvaru lze zobecnit na součin
libovolného počtu činitelů: 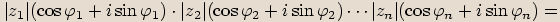
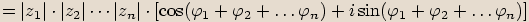 .
.
Poznámka
Součin komplexního čísla a reálného čísla v Gaussově rovině má stejný argument jako dané komplexní číslo (protože reálné číslo má argument rovný nule a při násobení se argumenty sčítají) a jeho absolutní hodnota je součinem absolutních hodnot obou čísel.
Poznámka
Obraz součinu komplexního čísla a komplexní jednotky sestrojíme tak, že obraz tohoto čísla otočíme kolem počátku soustavy souřadnic o argument komplexní jednotky.
Příklady
 a výsledky zapište i v algebraickém tvaru.
a výsledky zapište i v algebraickém tvaru.
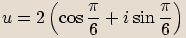 ,
, 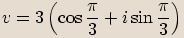

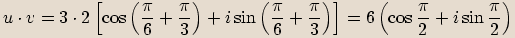

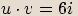

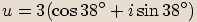 ,
, 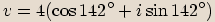

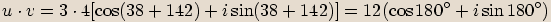



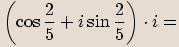

 převedeme do goniometrického tvaru.
převedeme do goniometrického tvaru.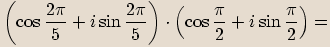

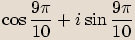

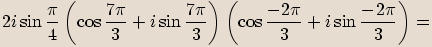

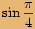 .
.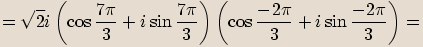

 převedeme do goniometrického tvaru.
převedeme do goniometrického tvaru.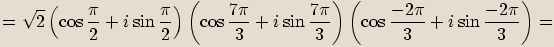

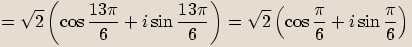

Reciproké číslo
Definice
Reciproká čísla
Reciprokým číslem ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 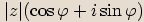 nazveme číslo
nazveme číslo
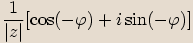 .
Toto reciproké číslo označujeme
.
Toto reciproké číslo označujeme  .
.

 a
a nazýváme reciproká, jestliže jejich absolutní
nazýváme reciproká, jestliže jejich absolutníhodnoty jsou navzájem převrácená čísla a jejich argumenty se liší
znaménkem, tj. 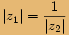 a
a  .
.
Poznámka
Navzájem reciproká čísla musí mít opačný argument, protože při násobení se argumenty sčítají a
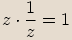 . Součet jejich argumentů tedy musí dát nulu, protože
. Součet jejich argumentů tedy musí dát nulu, protože 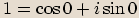 .
.
Poznámka
Protože sinus a kosinus jsou funkce s periodou 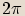 , k číslu
, k číslu 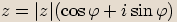 jsou reciproká
jsou reciproká
všechna čísla
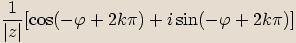 , kde
, kde 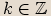 .
.
Poznámka
Čísla 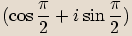 a
a 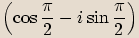 jsou navzájem komplexně sdružená, opačná i reciproká.
jsou navzájem komplexně sdružená, opačná i reciproká.
Příklady
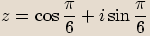

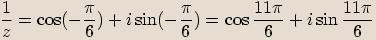

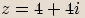

 převedeme do goniometrického tvaru.
převedeme do goniometrického tvaru.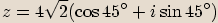

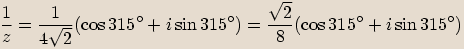

Dělení komplexních čísel v goniometrickém tvaru
Vydělíme-li nenulový výraz 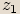 , který se rovná
, který se rovná 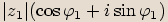 , nenulovým výrazem
, nenulovým výrazem 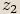 , který se rovná
, který se rovná 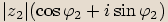 , dostáváme následující vztah
, dostáváme následující vztah
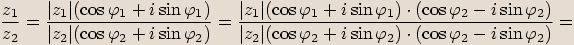
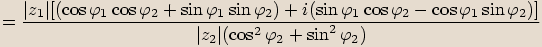 .
.
Použijeme-li součtové vzorce pro sinus a kosinus  ,
,  a
a  ,
,
dostáváme 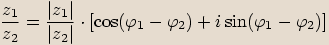 .
.
Pokud budeme oba výrazy 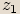 a
a 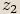 chápat jako komplexní čísla zapsaná v
goniometrickém tvaru, povede nás to k následující definici.
chápat jako komplexní čísla zapsaná v
goniometrickém tvaru, povede nás to k následující definici.
Definice
Podíl dvou komplexních čísel
Máme-li dvě nenulová komplexní čísla  a
a  , pak
jejich podílem nazveme komplexní číslo
, pak
jejich podílem nazveme komplexní číslo
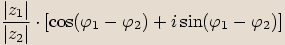 . Tento podíl
značíme
. Tento podíl
značíme 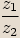 .
.

tvaru dostaneme tak, že vydělíme jejich absolutní hodnoty a odečteme
argumenty.
Věta
Pro každé 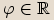 platí
platí 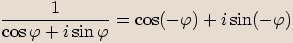 .
.

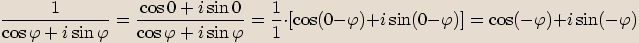

Příklady
 a výsledky zapište i v algebraickém tvaru.
a výsledky zapište i v algebraickém tvaru.
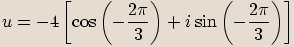 ,
, 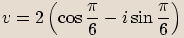

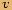 zapíšeme
zapíšemev goniometrickém tvaru.
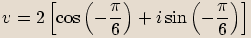

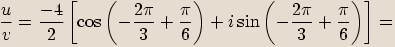
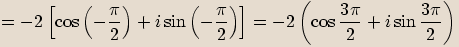

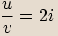

 ,
, 

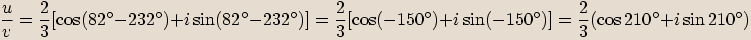

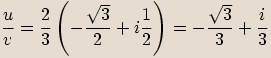



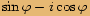 a vynásobíme.
a vynásobíme.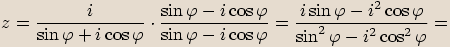



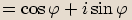

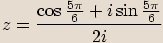

 zapíšeme v goniometrickém tvaru a spočítáme podíl.
zapíšeme v goniometrickém tvaru a spočítáme podíl.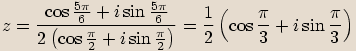

Poznámka
Pro komplexní čísla v goniometrickém tvaru je také možné zavést součet a rozdíl. Provádění těchto operací je však složité, musí se využívat součtové vzorce pro goniometrické funkce. Proto je zde definovat nebudeme a sčítat a odčítat budeme pouze čísla v algebraickém tvaru.
>>další stránka<<>>nahoru<<