n-tá mocnina komplexního čísla
Definice
Mocnina komplexního čísla
n-tou mocninou komplexního čísla  , kde
, kde 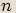 je přirozené číslo,
rozumíme součin
je přirozené číslo,
rozumíme součin 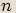 čísel
čísel  .
.

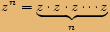
Věta
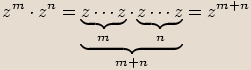
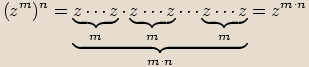
Pro libovolná komplexní čísla 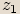 ,
, 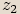 ,
, 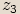 a přirozená čísla
a přirozená čísla 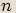 ,
, 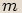 platí následující vlastnosti:
platí následující vlastnosti:
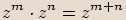


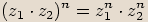

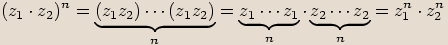

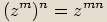


Poznámka
Na začátku kapitoly bylo uvedeno, že pro imaginární jednotku platí 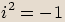 .
.
Věta
Pro mocniny imaginární jednotky platí následující vlastnosti:
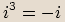

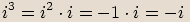



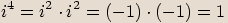

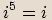

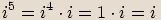

Poznámka
Obecně pro libovolné přirozené 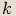 platí:
platí:
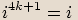
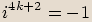
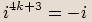
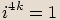

|
|
|
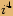
|

|
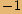
|
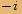
|
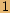
|
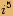
|
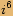
|
... |

|
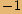
|
... |
Poznámka
Počítáme-li druhou nebo třetí mocninu komplexního čísla 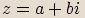 v algebraickém
tvaru, můžeme použít vzorce
v algebraickém
tvaru, můžeme použít vzorce 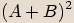 nebo
nebo 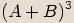 .
.
Poznámka
Chceme-li vypočítat 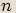 -tou mocninu komplexního čísla
-tou mocninu komplexního čísla 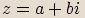 v algebraickém
tvaru, lze
v algebraickém
tvaru, lze
použít binomickou větu 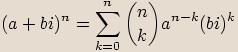 , kde
, kde 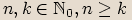 .
.
Tento postup však může být v případě vyšších mocnin poměrně dlouhý a obtížný. Proto se pro umocňování komplexních čísel používá místo algebraického tvaru tvar goniometrický, kterému se budeme věnovat později. n-tá mocnina komplexního čísla v goniometrickém tvaru
Definice
n-tou mocninu komplexního čísla 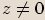 , kde
, kde 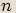 je celé záporné číslo,
definujeme jako
je celé záporné číslo,
definujeme jako
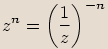 .
Pro libovolné komplexní číslo
.
Pro libovolné komplexní číslo 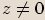 definujeme
definujeme 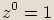 .
.
Poznámka
Součet druhých mocnin reálných čísel lze v oboru komplexních čísel vyjádřit jako součin:
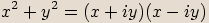
Poznámka
V oboru  obecně neplatí rovnost
obecně neplatí rovnost 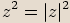 , kde
, kde
 . Pro každé
. Pro každé  je totiž
je totiž 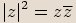 ,
a proto zmíněná rovnost
,
a proto zmíněná rovnost 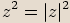 platí pouze pro čísla, pro něž
platí pouze pro čísla, pro něž  ,
to znamená pro čísla reálná.
,
to znamená pro čísla reálná.
Příklady
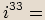

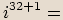

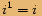 ,
, 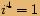

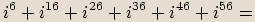

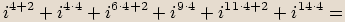

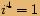 ,
, 


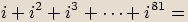

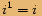 ,
,  ,
,
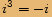 ,
, 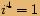


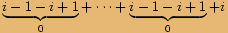
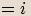

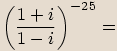

 .
.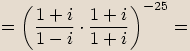

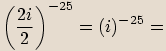

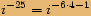
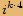 , kde
, kde 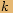 je celé číslo, je rovno jedné.
je celé číslo, je rovno jedné.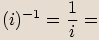

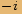 .
.

 .
.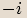

n-tá odmocnina z komplexního čísla
Definice
Odmocniny komplexního čísla
n-tou odmocninou z komplexního čísla 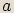 , kde
, kde 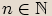 , nazveme
každé takové komplexní číslo
, nazveme
každé takové komplexní číslo  , pro které platí
, pro které platí 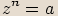 .
.

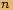 -tou odmocninu
-tou odmocninuz komplexního čísla
 ,
stačí vyřešit rovnici
,
stačí vyřešit rovnici  .
. Poznámka
Je-li  , má rovnice
, má rovnice 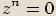 právě jedno řešení
právě jedno řešení  , takže
, takže 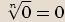 . Je-li
. Je-li
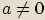 , rovnice
, rovnice 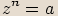 má v oboru komplexních čísel právě
má v oboru komplexních čísel právě 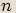 různých řešení, která lze určit pomocí
goniometrického tvaru komplexního čísla. Postup při určování těchto řešení uvidíme dále.
různých řešení, která lze určit pomocí
goniometrického tvaru komplexního čísla. Postup při určování těchto řešení uvidíme dále.
Poznámka
(Komplexní) 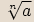 pro každé
pro každé 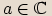 ,
, 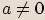 , je
, je 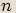 -značná, nabývá právě
-značná, nabývá právě 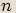 různých komplexních hodnot.
Tím se odlišuje od (reálné)
různých komplexních hodnot.
Tím se odlišuje od (reálné) 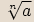 pro
pro 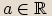 . (Reálná)
. (Reálná) 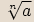 pro
pro 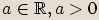 , je totiž jednoznačná, nabývá právě jedné nezáporné hodnoty.
(Reálná)
, je totiž jednoznačná, nabývá právě jedné nezáporné hodnoty.
(Reálná) 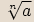 pro
pro 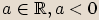 , je definována pouze pro
, je definována pouze pro 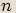 lichá.
lichá.