Základní kombinatorická pravidla

Řešené příklady

Příklad 1

Určete počet všech přirozených dvojciferných čísel, v jejichž dekadickém zápisu se každá číslice vyskytuje nejvýše jednou.

Řešení

V tomto případě lze využít obě kombinatorická pravidla.

1) Řešení s využitím kombinatorického pravidla součinu

Na místě desítek může být libovolná z číslic \(1,2,\ldots,9\), máme tedy devět možností pro výběr první číslice. Ke každé z nich existuje devět možností, jak vybrat číslici pro místo jednotek: může zde být číslice \(0\) a libovolná z číslic \(1,2,\ldots,9\), která je různá od číslice stojící na místě desítek. Celkem lze tedy sestavit \(9 \cdot 9 = 81\) uvažovaných dvojciferných čísel.

2) Řešení s využitím kombinatorického pravidla součtu

Všechna přirozená dvojciferná čísla lze rozdělit do dvou disjunktních skupin tak, že v první jsou dvojciferná čísla s různými číslicemi a ve druhé dvojciferná čísla se stejnými číslicemi.
Počet všech dvojciferných čísel je \(90\), počet dvojciferných čísel se stejnými číslicemi je \(9\) (jsou to čísla \(11, 22, \ldots, 99\)). Označíme-li hledaný počet dvojciferných čísel s různými číslicemi \(x\), pak platí:

\(x+9=90\).

Odtud dostáváme, že je \(x=81\).

Příklad 2

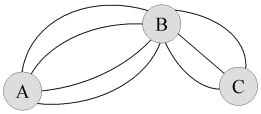Z místa A do místa B vedou čtyři turistické cesty, z místa B do C tři. Určete, kolika způsoby lze vybrat trasu z A do C a zpět tak, že z těchto sedmi cest je právě jedna použita dvakrát.

Řešení

Nejprve určíme, kolika způsoby lze vybrat trasu z A do C: ke každému ze čtyř způsobů, jak dojít z A do B, existují tři způsoby, jak dojít z B do C. Trasu z A do C lze tedy vybrat \(4 \cdot 3\), tj. dvanácti způsoby.

Nyní jde o to, kolika způsoby lze vybrat zpáteční trasu z C do A tak, aby v ní byla použita právě jedna cesta z těch, po kterých jsme už šli z A do C. Máme tedy dvě možnosti:

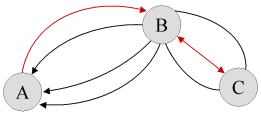
1. Po stejné cestě se budeme vracet z C do B. Potom z B do A půjdeme jinou cestou, než kterou jsme šli z A do B. V tomto případě lze vybrat zpáteční trasu z C do A třemi způsoby.
   
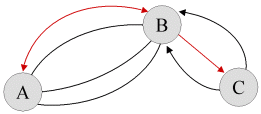
2. Z C do B půjdeme jinou cestou, než kterou jsme přišli, a z B do A půjdeme po stejné cestě, jako z A do B. V tomto případě lze vybrat zpáteční trasu z C do A dvěma způsoby.
   

Protože obě uvedené možnosti se navzájem vylučují a jiné nejsou, dostáváme (podle kombinatorického pravidla součtu), že celkový počet tras z C do A, které splňují dané podmínky, je roven pěti.
Ke každé z dvanácti tras z A do C existuje tedy pět tras z C do A, které splňují požadovanou podmínku. Pomocí kombinatorického pravidla součinu získáme výsledek úlohy: počet všech způsobů, kterými lze vybrat trasu z A do C a zpět tak, že z daných cest je právě jedna použita dvakrát, je \(12 \cdot 5 = \boldsymbol{60}\).

Podobné úlohy

Určete počet způsobů, jimiž lze vybrat trasu

a) z A do C a zpět; [výsledek: \(4 \cdot 3 \cdot 3 \cdot 4 = \boldsymbol{144}\)]

b) z A do C a zpět tak, že z těchto sedmi cest není žádná použita dvakrát; [výsledek: \(4 \cdot 3 \cdot 2 \cdot 3 = \boldsymbol{72}\)]

c) z A do C a zpět tak, že z těchto sedmi cest jsou právě dvě použity dvakrát. [výsledek: \(4 \cdot 3 \cdot 1 \cdot 1 = \boldsymbol{12}\)]