\begin{align} \end{align}


1.2 Druhá odmocnina z reálného čísla

Definice

Druhá odmocnina z nezáporného reálného čísla \(a\) je nezáporné reálné číslo \(b\), pro které platí, že \(b \cdot b = a\). Značíme \(b = \sqrt{a \;}\).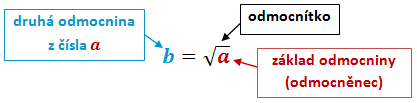
Číslo \(a\) označujeme jako základ odmocniny (odmocněnec), symbol \(\sqrt{\; \; \;}\) se nazývá odmocnítko.
odmocnina

Říkáme, že "odmocněním čísla \(a\) dostaneme číslo \(b\)".

Z definice vyplývají dvě důležitá tvrzení.

1. Druhá odmocnina je definována pouze z nezáporného čísla.
2. Druhá odmocnina je vždy nezáporná.
Druhá vlasnost zaručuje jednoznačnost. Přestože platí \(3 \cdot 3 = 9\) a zároveň \((- \, 3) \cdot (- \, 3) = 9\), druhá odmocnina
z devíti je dle definice vždy nezáporné číslo, proto \(\sqrt{9 \;} = 3\).

Příklad 1.4

Odmocni:
a) \(\sqrt{16 \;}\) b) \(\displaystyle \sqrt{\frac{1} {25}}\) c) \(\sqrt{- \, 4 \;}\) d) \(\sqrt{0,01 \;}\)

Řešení

a) \(\sqrt{16 \;} = 4\), protože \(4 \cdot 4 = 16\).

b) \(\displaystyle \sqrt{\frac {1} {25} \;} = \frac {1} {5}\), protože \(\displaystyle \frac {1} {5} \cdot \frac {1} {5} = \frac {1} {25}\).

c) Tato odmocnina není v oboru reálných čísel definována. Lze určit jen odmocninu z nezáporného čísla.

d) \(\sqrt{0,01 \;} = 0,1\), protože \(0,1 \cdot 0,1 = 0,01\).


Pro všechna nezáporná reálná čísla \(a\), \(b\) platí:
1. \( \; \sqrt{a \cdot b \;} = \sqrt{a \;} \cdot \sqrt{b \;}\) 2. \(\; a \cdot \sqrt{b \;} = \sqrt{a \cdot a \cdot b \;}\) 3. \(\displaystyle \; \sqrt{\frac {\; a \;}{b} \;} = \frac{\sqrt{a \;}}{\sqrt{b \;}}\) pro \(b \neq 0\)

Příklad 1.5

Odmocni:
a) \(\displaystyle \sqrt{\frac {\; 64 \;}{49} \;}\) b) \(\sqrt{0,04 \;}\) c) \(\sqrt{3 \cdot 81 \cdot 12 \;}\) d) \(\sqrt{75 \;}\)

Řešení

a) \(\displaystyle \sqrt{\frac {\; 64 \;}{49} \;} = \frac {\sqrt{64 \;}} {\sqrt {49 \;}} = \frac {8} {7}\)

b) \(\sqrt{0,04 \;} = \sqrt{0,01 \cdot 4 \;} = \sqrt{0,01 \;} \cdot \sqrt{4 \;} = 0,1 \cdot 2 = 0,2\)

c) \(\sqrt{3 \cdot 81 \cdot 12 \;} = \sqrt{81 \;} \cdot \sqrt{3 \cdot 12 \;} = 9 \cdot \sqrt{36} = 9 \cdot 6 = 54\)

d) \(\sqrt{75 \;} = \sqrt {25 \cdot 3} = 5 \cdot \sqrt{3}\)


V příkladu 1.5 d) jsme provedli částečné odmocnění.