3.1 Výrazy
S výrazy se v matematice běžně setkáváme, jsou to např. \(3a + 5\), \(x^{-2} - 12\), \((x - y)^2\), \(\sqrt {72(x^3 + y)}\). Vyskytují se v nich konkrétní čísla (např. \(3\), \(5\), \(-\,12\), \(72\)), která označujeme jako konstanty, ale také reprezentanti čísel, tzv. proměnné (např. \(a\), \(x\), \(y\)). Proměnné, které zapisujeme libovolnými písmeny, zastupují čísla z určitého číselného oboru. Tento obor nazýváme obor proměnné. Např. ve výrazu \(u - 2\) zastupuje proměnná \(u\), jejíž obor proměnné jsou přirozená čísla, čísla 1, 2, 3, 4, atd. Tento výraz tak po dosazení konkrétních hodnot za proměnnou (z oboru proměnné) lze napsat následovně: \(1 - 2\), \(2 - 2\), \(3 - 2\), \(4 - 2\), atd. Konstanty a proměnné jsou ve výrazech svázány prostřednictvím matematických operací.
Definice
Algebraický výraz je každý matematický zápis, který je tvořen z konstant a proměnných, mezi nimiž jsou pomocí algebraických operací (např. sčítání, násobení) a závorek vytvořeny smysluplné vztahy.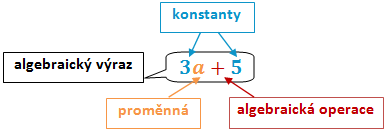
Výrazem není zápis \(7^2 - (2-\) či \(5a^3 +\), protože nesplňuje požadavek smyslupnosti z definice.
Poznámka
Opačným výrazem k výrazu \(\displaystyle \frac {(a - 1)^3 + 4} {5}\) je výraz \(\displaystyle - \, \frac {(a - 1)^3 + 4} {5}\) .Poznámka
V této kapitole pracujeme s algebraickými výrazy, tj. s výrazy, v nichž za každou proměnnou dosazujeme z číselného oboru. Existují ale i nealgebraické výrazy, jako je výraz \(\mathbb A \cap \mathbb B\).S nealgebraickými výrazy se setkáváme např. ve výrokové logice. Většinou lze z kontextu poznat, kdy výraz je či není algebraický. Proto můžeme slovo algebraický vynechat.
Příklad 3.1
Řešení
Pomocí výrazu \(2 \pi r\) lze vypočítat obvod kruhu.
Konstantami jsou čísla \(2\) a \(\pi\) (jejich hodnota je stále stejná, konstantní).
Proměnnou je v tomto případě písmeno \(r\), vyjadřující poloměr daného kruhu
(poloměr se pro různé kruhy může měnit, proměňovat, a s ním i obvod kruhu).
A jaký je obor proměnné \(r\) pro výraz \(2 \pi r\)? Díváme-li se na tento výraz jako
na vztah pro výpočet obvodu kruhu, tak obor proměnné je tvořen všemi kladnými reálnými čísly (poloměr kruhu, tedy
proměnná \(r\), nemůže nabývat záporných hodnot ani nuly). Jestliže však výraz \(2 \pi r\) chápeme obecněji, jako výraz se dvěma konstantami a jednou proměnnou, pak do oboru proměnné zahrnujeme
všechna reálná čísla.
Poznámka
Pozorný čtenář jistě zpozoroval, že řecké písmeno \(\pi\) [pí] jsme označili jako konstantu. Jak už vímez tématu o číselných oborech, symbol \(\pi\) reprezentuje iracionální Ludolfovo číslo (jeho přibližná
hodnota je 3,14).
Při řešení příkladů, ve kterých se objevují výrazy, je třeba dbát na to, abychom neprováděli nepřípustné operace (např. dělení nulou, umocňování nuly na nultou, odmocňování záporného čísla v oboru reálných čísel, atd.).
Definice
Hodnotou výrazu pro dané hodnoty proměnných rozumíme výsledek získaný po dosazení těchto hodnot za všechny proměnné a provedení veškerých přípustných operací.
Příklad 3.2
| a) \(\displaystyle \frac {a + 5}{4 - a}\), pro \(a = 3\) | b) \(\displaystyle x^2 \cdot \sqrt {y - 2\;}\), pro \(x = -\,2\), \(y = 6\) |
| c) \(\displaystyle \frac {|k - 5|}{(l + 1)^2 \cdot \sqrt {k\;}}\), pro \(k = 4\), \(l = 2\) | d) \(\displaystyle \frac {\sqrt {6 - p\;}}{|-2 + q|}\), pro \(p = 5\), \(q = 2\) |
Řešení
a) Po dosazení \(a = 3\) do výrazu dostaneme:
\(\displaystyle \; \; \; \frac {3 + 5}{4 - 3} = \frac {8}{1} = 8\)
b) Po dosazení \(x = - \,2\), \(y = 6\) do výrazu dostaneme:
\(\displaystyle \; \; \; (-\,2)^2 \cdot \sqrt {6 - 2\;} = 4 \cdot \sqrt {4} = 4 \cdot 2 = 8\)
c) Po dosazení \(k = 4\), \(l = 2\) do výrazu dostaneme:
\(\displaystyle \; \; \; \frac {|4 - 5|}{(2 + 1)^2 \cdot \sqrt {4\;}} =
\frac {|-1|}{3^2 \cdot 2} = \frac {1}{9 \cdot 2} = \frac {1}{18}\)
d) Pro zadané hodnoty proměnných nelze určit hodnotu výrazu. Po dosazení za proměnnou \(q\) ve jmenovateli
by nastala nepřípustná operace, a to dělení nulou.
Kromě oboru proměnné zavádíme i definiční obor proměnné. Nejprve si však musíme říct, za jakých podmínek má výraz smysl.
Definice
Do definičního oboru proměnné patří jen taková čísla z oboru proměnné, pro které má výraz smysl.Příklad 3.3
Řešení
Pokud výraz \(2 \pi r\) chápeme jako vztah pro výpočet obvodu kruhu, pak je definiční obor
proměnné \(r\) tvořen všemi kladnými reálnými čísly.
Jestliže však výraz \(2 \pi r\) chápeme obecněji, jako výraz se dvěma konstantami a jednou proměnnou,
pak do definičního oboru patří všechna reálná čísla.
Do definičního oboru proměnné v tomto příkladu tedy patří všechny hodnoty z oboru proměnné, což ovšem neplatí vždy.
Poznámka
Není-li v zadání úlohy obor proměnné uveden, bereme obvykle v úvahu obor reálných čísel. Pak mluvíme o tzv. reálné proměnné. Z tohoto oboru vynecháme ty hodnoty, pro které výraz nemá smysl, a tím dostaneme definiční obor proměnné.Poznámka
Do definičního oboru výrazu s více proměnnými patří jen taková čísla, pro která má daný výraz smysl.
Příklad 3.4
| a) \(\displaystyle V_1 = \frac {1 + x}{2 - x}\) | b) \(\displaystyle V_2 = \frac {x \cdot \sqrt{x - 5\;}}{y^2 - 9}\) | c) \(\displaystyle V_3 = \frac {\sqrt {x^2 + 2\;}}{\sqrt {y + 3\;} \cdot \left(|z - 6| - 2\right)}\) |
Řešení
a) Výraz \(V_1\) obsahuje proměnnou \(x\).
- Výraz má smysl, pokud je jmenovatel nenulový (v opačném případě by nastala nepřípustná operace dělení nulou).
Výraz tedy má smysl pro všechna \(x \in \mathbb R\), pro která je \(2 - x \neq 0\), tj. \(x \neq 2\). - Podmínky: \(x \in \mathbb R - \{2\}\)
- Pro proměnnou \(x\) musí platit, že \(x - 5 \geq 0\), tj. \(x \geq 5\).
Zaručíme tím, že odmocňujeme nezáporné číslo. - Zároveň pro proměnnou \(y\) musí platit, že \(y^2 - 9 \neq 0\), tedy \(y^2 \neq 9\), tj. \(y \neq \pm 3\).
Tím vyloučíme případ dělení nulou. - Podmínky: \(x \in \mathbb R \wedge x \geq 5\), \(y \in \mathbb R - \{\pm 3\}\)
- Pro proměnnou \(x\) musí platit, že \(x^2 + 2 \geq 0\), tj. \(x^2 \geq -\,2\).
V opačném případě bychom odmocňovali záporné číslo, což je v oboru reálných čísel nepřípustná operace.
Uvedenou podmínku splňují všechna \(x \in \mathbb R\), protože druhá mocnina libovolného čísla je vždy větší nebo rovna nule. - Zároveň musí pro proměnnou \(y\) platit, že \(y + 3 > 0\), tj. \(y > -\,3\).
Musíme totiž zaručit, že výraz pod odmocninou je nezáporné číslo a zároveň že je jmenovatel nenulový (přitom platí, že součin je roven nule právě tehdy, když alespoň jeden z činitelů je roven nule). Výraz pod odmocninou tedy musí být kladné číslo. - Také druhý činitel ve jmenovateli musí být různý od nuly, aby měl výraz smysl.
Pro proměnnou \(z\) tedy musí platit, že \(| z - 6 | - 2 \neq 0\), tj. \(|z - 6| \neq 2\), tedy \(z \neq 4 \wedge z \neq 8\). - Podmínky: \(x \in \mathbb R\), \(y \in \mathbb R \wedge y > -\,3\), \(z \in \mathbb R - \{4,8\}\)
S výrazy se v matematickém textu setkáváme často. Výraz totiž nahrazuje zdlouhavý slovní popis. Srovnej: Podíl pětinásobku součtu dvou reálných čísel a druhé odmocniny z jejich rozdílu jednoduše zapíšeme jako \(\displaystyle \frac {5(x \,+ \,y)}{\sqrt {x \,- \,y}}\) .
Příklad 3.5
a) součet šestinásobku třetí mocniny prvního čísla a třetiny absolutní hodnoty druhého čísla
b) rozdíl druhé odmocniny z dvojnásobku prvního čísla a druhé mocniny čtyřnásobku druhého čísla
c) součin dvojnásobku prvního čísla a čtvrtiny druhé odmocniny z druhého čísla
d) podíl čtvrté mocniny prvního čísla a absolutní hodnoty dvojnásobku druhého čísla
e) rozdíl \(25\, \%\) ze základu \(z\) a trojnásobku \(18 \, \%\) z tohoto základu
Řešení
| a) \(\displaystyle 6x^3 + \frac {1}{3}|y|\) | b) \(\displaystyle \sqrt {2x\;} - (4y)^2\) | c) \(\displaystyle 2x \cdot \frac {1}{4} \sqrt {y}\) | d) \(\displaystyle \frac {x^4}{|2y|}\) | d) \(\displaystyle 0,25z - 3 \cdot 0,18z\) |
S výrazy se setkáváme také v souvislosti se vzorci, a to nejen v matematice, ale i v dalších
vědách - fyzice, chemii, zeměpisu (např. vzorec pro objem kvádru, výpočet rychlosti podle dráhy a času,
vzdálenost dvou míst na Zemi podle jejich souřadnic). Výrazy nám pomáhají i při zápisu řešení slovních úloh.
Příklad 3.6
Třída 2.B, do které chodí 24 žáků, měla naplánovanou školní exkurzi. Uvažujme, že pokladník na dopravu dohromady vybral \(k\) Kč (což je cena za 24 zpátečních obyčejných jízdenek) a předal je učiteli. V den exkurze se 3 žáci nedostavili. Učitel využil množstevní slevu a koupil pro přítomné žáky hromadnou zpáteční jízdenku. Tím ušetřil čtvrtinu z celkové vybrané částky, přičemž každý zúčastněný žák ušetřil 9 Kč oproti původnímu plánu. Jakou částku vybral celkově pokladník? Jakou částku vybíral od každého spolužáka?
Řešení
Počet žáků ve třídě \(\dots\) 24
Celková cena za dopravu \(\dots\) \(k\) Kč
Původní cena za dopravu na žáka \(\dots\) \(\frac {k} {24}\) Kč
Celková cena za dopravu po slevě \(\dots\) \(0,75k\) Kč
Skutečná cena za dopravu na žáka \(\dots\) \(\frac {0,75k} {21}\) Kč
Rozdíl původní a skutečné ceny za dopravu na žáka \(\dots\) \(9\) Kč, tedy
\(\displaystyle \; \; \; 9 = \frac {k} {24} - \frac {0,75k} {21}\)
\(\displaystyle \; \; \; 9 = \frac {21k - 24 \cdot \frac {3} {4}k} {504} = \frac {21k - 18k} {504} = \frac {3k} {504} = \frac {k} {168}\)
\(\displaystyle \; \; \; k = 168 \cdot 9 = 1\,512\)
Původní cena na žáka \(\dots \) \(\displaystyle \frac {k} {24} = \frac {1\,512} {24} = 63\) Kč.
Pokladník celkově vybral \(1\,512\) Kč. Od každého spolužáka vybíral \(63\) Kč.
Cvičení k této části.
