Věta o polovičních úhlech Další trigonometrické věty Poloměr kružnice opsané trojúhelníku Obsah trojúhelníku pomocí dvou stran a úhlu jimi sevřeném Heronův vzorec Poloměr kružnice opsané pomocí obsahu trojúhelníku a jeho tří stran Poloměr kružnice vepsané pomocí obsahu trojúhelníku a jeho tří stran Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Další trigonometrické věty
Vztah pro poloměr kružnice opsané trojúhelníku
Pro poloměr 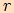 kružnice opsané trojúhelníku
kružnice opsané trojúhelníku 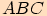 platí
platí 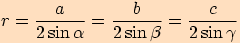 .
.
Kružnice opsaná trojúhelníku
s počítáním poloměru
Důkaz
 Označme
Označme 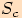 střed strany
střed strany 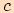 .
Trojúhelník
.
Trojúhelník 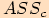 je pravoúhlý s pravým
úhlem u vrcholu
je pravoúhlý s pravým
úhlem u vrcholu 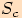 .
Velikost úhlu
.
Velikost úhlu 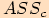 je
je 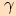 ,
je-li
,
je-li 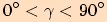 ,
nebo
,
nebo 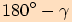 pro
pro 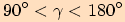 .
.
V obou případech tedy platí
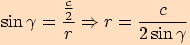 .
.
Zbývá uvážit pravoúhlý trojúhelník 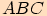 s pravým
úhlem u vrcholu
s pravým
úhlem u vrcholu 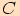 , strana
, strana
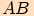 je průměrem kružnice
je průměrem kružnice 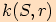 ,
která je opsaná tomuto trojúhelníku.
Jinak řečeno
,
která je opsaná tomuto trojúhelníku.
Jinak řečeno 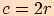 a
a
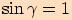 .
Za těchto předpokladů opět platí vztah
.
Za těchto předpokladů opět platí vztah 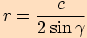 .
.
Další vyjádření pro poloměr kružnice opsané dostaneme cyklickou záměnou.
Příklady
1.
V trojúhelníku 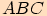 je
je 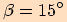 ,
,
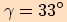 , poloměr kružnice tomuto trojúhelníku opsané je
, poloměr kružnice tomuto trojúhelníku opsané je
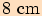 .
.
Vypočítejte délky stran trojúhelníku.

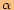 .
.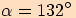

pro poloměr opsané kružnice.
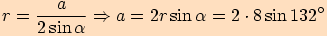
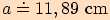

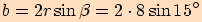
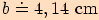

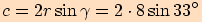
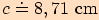

2.
Vypočítejte obvod trojúhelníku, který je vepsán do kružnice o poloměru
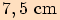 a jehož dva vnitřní úhly mají velikosti
a jehož dva vnitřní úhly mají velikosti 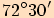 a
a
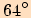 .
.

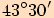

na poloměru kružnice opsané.
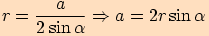

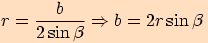

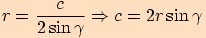

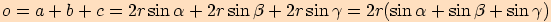

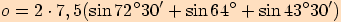
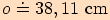

>>nahoru<<
Obsah trojúhelníku pomocí dvou stran a úhlu jimi sevřeném
Pro obsah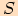 každého trojúhelníku
každého trojúhelníku
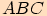 ,
jehož vnitřní úhly mají velikosti
,
jehož vnitřní úhly mají velikosti 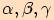 a strany mají délky
a strany mají délky
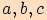 platí
platí 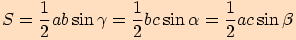 .
. Obsah trojúhelníku
Důkaz

Vyjdeme ze vzorce pro výpočet obsahu trojúhelníku 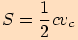 ,
kde
,
kde 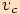 je výška na stranu
je výška na stranu 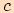 .
Označme
.
Označme 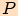 patu kolmice výšky
patu kolmice výšky 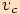 .
.
1)
Je-li trojúhelník 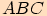 ostroúhlý, tedy
ostroúhlý, tedy
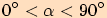 , pak
, pak
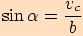 , tj.
, tj. 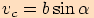 a
tudíž
a
tudíž 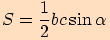 .
.
2)
Je-li trojúhelník 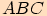 pravoúhlý,
tedy
pravoúhlý,
tedy 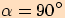 ,
pak
,
pak 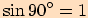 tudíž
tudíž 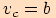 ,
,
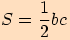 .
.
3)
Je-li trojúhelník 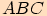 tupoúhlý, tedy
tupoúhlý, tedy
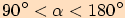 ,
pak
,
pak 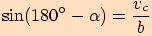 ,
přičemž levá strana se dá upravit takto
,
přičemž levá strana se dá upravit takto 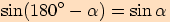 (viz Vzorce pro goniometrické funkce).
(viz Vzorce pro goniometrické funkce).
Jestliže nyní dosadíme do původního vzorce, získáme vyjádření obsahu
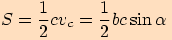 .
.
Další vzorce dostaneme cyklickou záměnou. 
Příklady
1.
Vypočítejte obsah 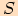 trojúhelníku
trojúhelníku
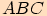 , jestliže
, jestliže
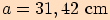 ,
,
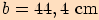 ,
,
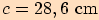 .
.

 .
.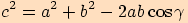

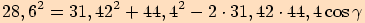

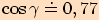



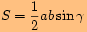
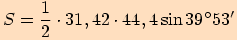
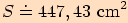

2.
Vypočítejte délky stran v trojúhelníku 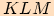 ,
jestliže
,
jestliže 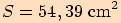 ,
,
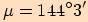 ,
,
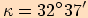 .
.

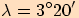

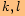 .
.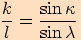

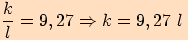

 .
.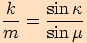

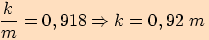

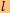 .
.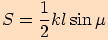

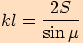

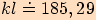

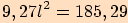

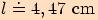

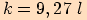
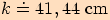

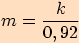
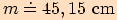

>>nahoru<<
Heronův vzorec
Pro obsah 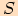 každého trojúhelníku
každého trojúhelníku 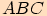 ,
jehož strany mají délky
,
jehož strany mají délky 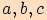 , platí
, platí
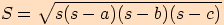 ,
kde
,
kde 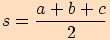 .
.
Důkaz

Vyjdeme z předchozí věty pro výpočet obsahu trojúhelníku 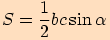 .
.
Vyjádříme 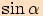 pomocí goniometrického vzorce
pomocí goniometrického vzorce
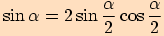 a za
a za 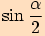 ,
,
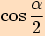 dosadíme vyjádření z věty o
dosadíme vyjádření z věty o
polovičních úhlech , čili 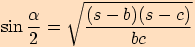 ,
, 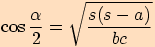 ,
kde
,
kde 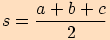 .
.
Po dosazení nám vyjde vztah 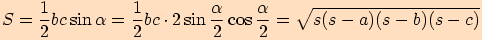 .
. 
Příklad
Vypočítejte pomocí Heronova vzorce obsah trojúhelníku 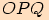 o stranách
o stranách 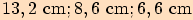 .
.

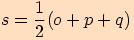
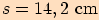

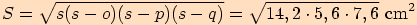
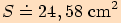

>>nahoru<<
Poloměr kružnice opsané pomocí obsahu trojúhelníku a jeho tří stran
Nechť 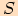 je obsah trojúhelníku
je obsah trojúhelníku 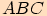 ,
jehož strany mají délky
,
jehož strany mají délky 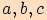 . Potom pro poloměr
. Potom pro poloměr
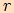 kružnice opsané tomuto trojúhelníku platí
kružnice opsané tomuto trojúhelníku platí
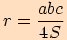 .
.
Kružnice opsaná trojúhelníku
Důkaz

Tento vzorec vyplývá ze sinové věty a z dříve dokázaného vztahu 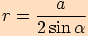 ,
kde
,
kde 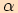 je velikost vnitřního úhlu v
je velikost vnitřního úhlu v
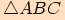 naproti straně
naproti straně 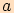 .
.
Jestliže dosadíme do vzorce
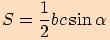 za
za 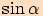 výraz
výraz 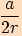 , dostaneme
, dostaneme 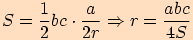 .
.

Příklad
Vypočítejte poloměr kružnice opsané trojúhelníku 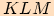 a stranách
a stranách 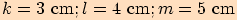 .
.

Vypočítáme jeho obsah (např. Heronovým vzorcem).
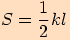
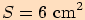

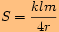
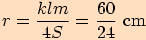
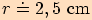

>>nahoru<<
Poloměr kružnice vepsané pomocí obsahu trojúhelníku a jeho tří stran
Nechť 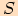 je obsah trojúhelníku
je obsah trojúhelníku 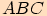 ,
jehož strany mají délky
,
jehož strany mají délky 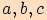 .
Potom pro poloměr
.
Potom pro poloměr 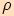 kružnice vepsané trojúhelníku
kružnice vepsané trojúhelníku 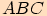 platí
platí
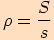 ,
kde
,
kde 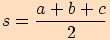 .
.
Kružnice vespaná trojúhelníku
Důkaz

Nechť 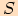 je střed kružnice vepsané
je střed kružnice vepsané
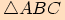 .
.
Protože 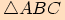 se skládá ze 3 nepřekrývajících
se trojúhelníků
se skládá ze 3 nepřekrývajících
se trojúhelníků 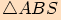 ,
, 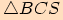 ,
,
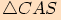 ,
je jeho obsah
,
je jeho obsah 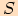 roven součtu obsahů těchto tří trojúhelníků, které mají stejnou výšku
roven součtu obsahů těchto tří trojúhelníků, které mají stejnou výšku
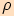 , tj.
, tj.
 .
.
Příklad
V trojúhelníku o stranách 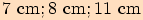 vypočítejte poloměr kružnice vepsané.
vypočítejte poloměr kružnice vepsané.

potřebujeme ješte hodnotu polovičního obvodu.
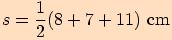
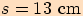

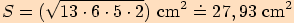

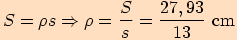

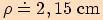

>>nahoru<<