Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Vzorce pro goniometrické funkce
V této poslední kapitole uvedeme přehled základních vztahů mezi jednotlivými goniometrickými funkcemi sinus, kosinus, tangens a kotangens a také připojíme jejich jednoduchý důkaz nebo alespoň poznámku, jak by se daný vztah odvodil.
Základní goniometrické vzorce
Věta. Pro každé 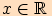 platí:
platí:
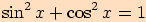

Applet k důkazu
Vezměme jednotkovou kružnici se středem v
počátku soustavy souřadnic, a vyznačme úhel o velikosti 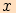 .
Bod, ve kterém protla polopřímka určující velikost úhlu
.
Bod, ve kterém protla polopřímka určující velikost úhlu 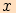 označíme
označíme 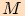 . Tento bod má souřadnice
. Tento bod má souřadnice
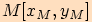 , kde souřadnice
, kde souřadnice
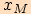 je funkční hodnota
je funkční hodnota  a
souřadnice
a
souřadnice 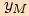 je funkční hodnota
je funkční hodnota 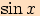 .
Vyznačíme ještě bod
.
Vyznačíme ještě bod 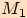 na ose
na ose 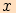 .
Z pravoúhlého trojúhelníka
.
Z pravoúhlého trojúhelníka 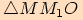 vyjádříme pomocí
Pythagorovy věty tuto rovnost
vyjádříme pomocí
Pythagorovy věty tuto rovnost 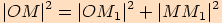 .
Odtud již plyne požadovaný vztah
.
Odtud již plyne požadovaný vztah 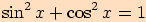 .
.

Věta. Pro každé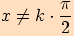 ,
,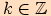 platí:
platí: 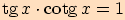

Funkce tangens a kotangens vyjádříme pomocí jejich definičních
vztahů z funkcí sinus a kosinus 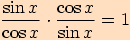 .
. 
>>nahoru<<
Součtové vzorce pro funkce pro sinus a kosinus
Věta. Pro každá dvě reálná čísla  ,
,
 platí:
platí:
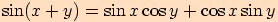
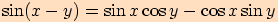
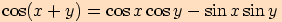
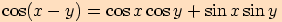

Vezměme dva jednotkové vektory 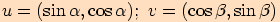 .
Podle jejich složek je zřejmé, že vektor
.
Podle jejich složek je zřejmé, že vektor 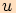 svírá
s osou
svírá
s osou  úhel
úhel  a vektor
a vektor 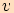 svírá s osou
svírá s osou
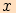 úhel
úhel
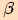 . Vektory
. Vektory 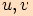 svírají úhel
svírají úhel 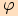 . Jestliže
si celou situaci nakreslíme, tak zjistíme, že platí
. Jestliže
si celou situaci nakreslíme, tak zjistíme, že platí 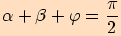 ,
tedy
,
tedy 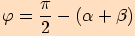 .
.
Z kapitoly
Goniometrické funkce ostrého úhlu
víme, že platí následující vztah 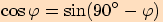 , tedy
v našem případě
, tedy
v našem případě 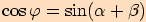 .
.
Úhel 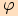 se vypočítá pomocí skalárního součinu
se vypočítá pomocí skalárního součinu
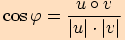 ,
,
 .
.
Vezmeme-li obě vyjádření
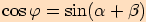 ,
,
 , vyjde nám požadovaná rovnost
, vyjde nám požadovaná rovnost
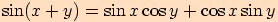 .
.
Ostatní vzorce bychom dokázali obdobně.

Užití součtových vzorců
Díky součtovým vzorcům umíme dokázat mimo jiné také tyto následující vztahy.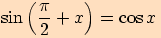
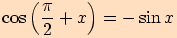
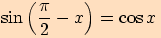
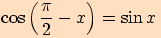
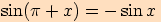
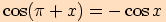
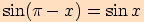
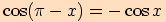

Dokážeme pouze první vztah, ostatní lze dokázat obdobně
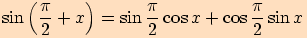
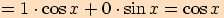 .
.

>>nahoru<<
Vzorce pro funkce sinus a kosinus argumentu 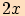 a
a
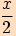
Věta. Pro každé reálné číslo 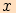 platí:
platí:
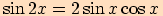

Tento vzorec snadno odvodíme ze součtového vzorce,
jestliže vezmeme součet (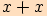 ).
Tedy
).
Tedy 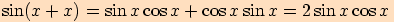 .
. 
Věta. Pro každé reálné číslo 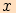 platí:
platí:
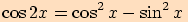

I tento vzorec odvodíme ze součtového vzorce, jestliže
vezmeme součet (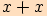 ).
Tedy
).
Tedy 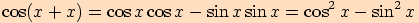 .
.

Věta. Pro každé reálné číslo 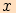 platí:
platí:
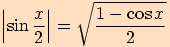

Nejprve vyjádříme funkci  jako součet polovičních úhlů, poté použijeme součtový vzorce
jako součet polovičních úhlů, poté použijeme součtový vzorce
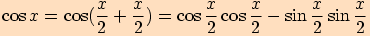
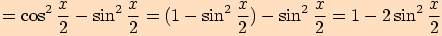 .
.
Vezmeme nyní první a poslední výraz a vyjádříme druhou mocninu sinu polovičního úhlu
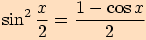 .
Odtud po odmocnění získáme požadovaný vztah
.
Odtud po odmocnění získáme požadovaný vztah 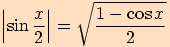 .
.

Věta. Pro každé reálné číslo 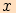 platí:
platí:
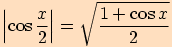

Postupujeme obdobně jako v důkazu předchozího vzorce. Vyjádříme funkci
 jako součet polovičních úhlů, poté použijeme součtový vzorce
jako součet polovičních úhlů, poté použijeme součtový vzorce 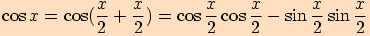 ,
,
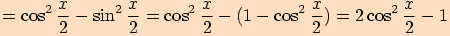 .
.
Tentokrát ovšem z prvního a posledního výrazu vyjádříme druhou mocninu kosinu polovičního úhlu
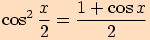 .
Nakonec celý vztah odmocníme
.
Nakonec celý vztah odmocníme 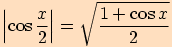 .
.

>>nahoru<<
Vzorce pro součet a rozdíl hodnot funkcí sinus a kosinus
Věta. Pro každá dvě reálná čísla 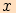 ,
,
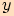 platí:
platí:
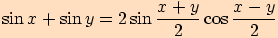
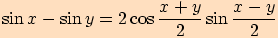

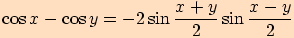

V důkazu těchto vzorců využijeme součtových vzorců a také toho,
že si takto šikovně rozepíšeme argumenty 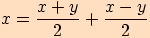 ,
,
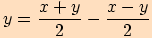 .
.
Ukážeme pouze důkaz prvního vztahu, přičemž ostatní dokážeme obdobně.
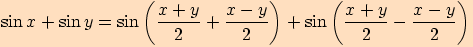
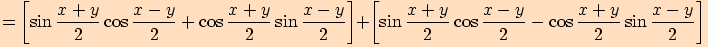
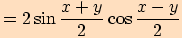

>>nahoru<<
Součtové vzorce pro funkci tangens
Věta. Pro každá dvě reálná čísla 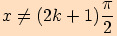 ,
,
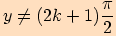 ,
,
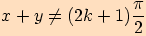 ,
,
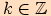 ,
,
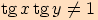
platí:
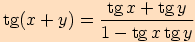

Využijeme součtových vzorců pro sinus a kosinus a dále upravujeme
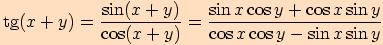
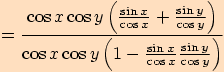
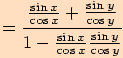
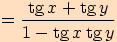 .
.

Věta. Pro každá dvě reálná čísla 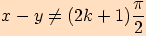 ,
kde
,
kde 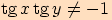 a
a
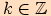
platí:
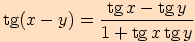

Stejně jako v předchozím důkazu využijeme součtových
vzorců pro sinus a kosinus 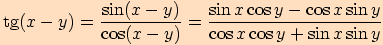
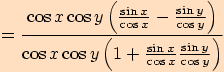
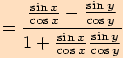
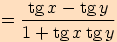 .
.
>>nahoru<<
Vzorce pro funkci tangens argumentů 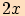 a
a
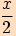
Věta. Pro každé reálné číslo 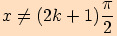 ,
,
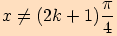 ,
kde
,
kde 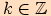 , platí:
, platí:
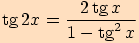

Funkci tangens vyjádříme dle definice pomocí funkcí sinus a kosinus
a dále využijeme vzorce pro dvojnásobné úhly těchto funkcí 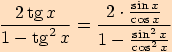
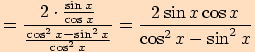
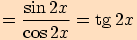

Věta. Pro každé reálné číslo 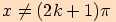 ,
kde
,
kde 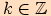 platí:
platí:
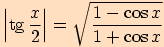

Tentokrát funkce sinus a kosinus vyjádříme
pomocí vzorců pro poloviční úhel 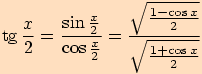 .
.
>>nahoru<<
Další vzorce
Věta. Pro každé reálné číslo 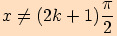 ,
kde
,
kde 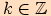 platí:
platí:
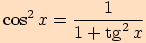

Tento vzorec lze dokázat pouze pomocí definice
funkce tangens, tj. podílem funkcí sinus a kosinus a jednoduché úpravy 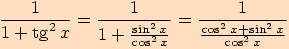
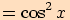

Věta. Pro každé reálné číslo 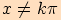 ,
,
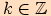 platí:
platí:
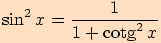

Obdobně tento vzorec dokážeme pomocí definice
funkce kotangens, tj. podílem funkcí kosinus a sinus 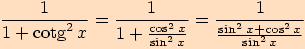
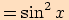

>>nahoru<<
Příklady
1. Upravte výraz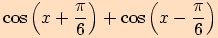 .
.




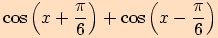

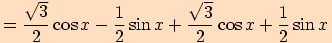

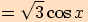

2. Upravte výraz
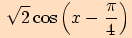 .
.
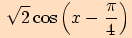

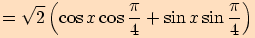

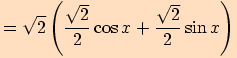

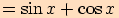

3.
Upravte výraz pomocí součtových vzorců 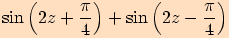 .
.

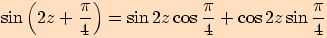

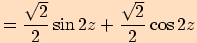

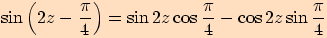

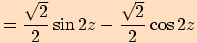

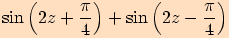

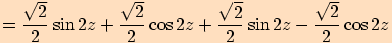

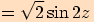

4.
Upravte výraz 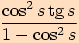 a stanovte podmínky.
a stanovte podmínky.

a podmínku, že ve jmenovateli nesmí být
 .
. 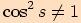 ,
,
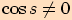 ,
tj.
,
tj. 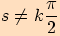

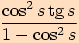
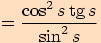

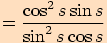



5.
Upravte výraz a stanovte podmínky 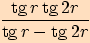 .
.

a podmínku, že ve jmenovateli nesmí být
 .
. 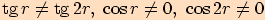 ,
tj.
,
tj. 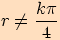

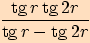




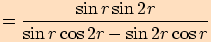

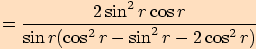

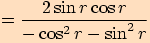



6.
Upravte výraz a stanovte podmínky 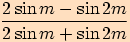 .
.

 .
. 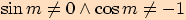 ,
tj.
,
tj. 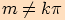

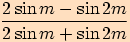
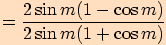

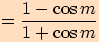

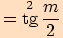

>>nahoru<<