Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Funkce sinus a kosinus
Zvolíme kartézskou soustavu souřadnic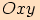 ,
tj. dvě na sebe kolmé číselné osy (osy
,
tj. dvě na sebe kolmé číselné osy (osy 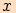 a
a
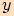 )
se společným počátkem
)
se společným počátkem 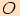 , přičemž na obou osách je
stejná délková jednotka. Vezměme bod
, přičemž na obou osách je
stejná délková jednotka. Vezměme bod 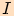 jako obraz čísla 1
na ose
jako obraz čísla 1
na ose 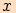 . Nyní sestrojíme orientovaný úhel o
velikosti
. Nyní sestrojíme orientovaný úhel o
velikosti 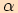 s počátečním ramenem
s počátečním ramenem 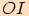 . Ke každému reálnému číslu
. Ke každému reálnému číslu
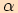 lze přiřadit právě jeden výše popsaný orientovaný úhel
lze přiřadit právě jeden výše popsaný orientovaný úhel 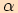 .
Tento orientovaný úhel se nazývá orientovaný úhel o velikosti
.
Tento orientovaný úhel se nazývá orientovaný úhel o velikosti 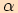 v základní poloze.
v základní poloze.
Definice funkcí sinus a kosinus pomocí jednotkové kružnice
Sestrojíme jednotkovou kružnici 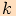 (tj. kružnice,
kde
(tj. kružnice,
kde 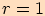 )
se středem
)
se středem 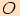 a označíme
a označíme 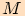 její průsečík
s koncovým ramenem orientovaného úhlu
její průsečík
s koncovým ramenem orientovaného úhlu 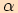 v základní poloze.
Bodem
v základní poloze.
Bodem 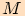 vedeme kolmici k ose
vedeme kolmici k ose 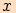 , jejich průsečík je
na ose
, jejich průsečík je
na ose 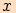 obrazem reálného čísla
obrazem reálného čísla 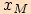 a dále
bodem
a dále
bodem 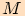 vedeme kolmici k ose
vedeme kolmici k ose 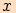 , jejich průsečík
je na ose
, jejich průsečík
je na ose 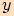 obrazem reálného čísla
obrazem reálného čísla 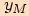 .
O číslech
.
O číslech 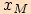 ,
,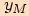 říkáme, že jsou první a druhou souřadnicí
bodu
říkáme, že jsou první a druhou souřadnicí
bodu 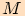 a píšeme
a píšeme 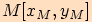 .
.
Definice. Druhou souřadnici bodu 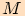 jednotkové kružnice na koncovém rameni orientovaného úhlu
jednotkové kružnice na koncovém rameni orientovaného úhlu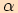 v základní poloze nazýváme sinus
v základní poloze nazýváme sinus 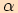 a jeho první souřadnici nazveme kosinus
a jeho první souřadnici nazveme kosinus 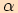 .
.
Používáme značení 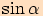 ,
,
 .Je tedy
.Je tedy 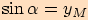 ,
,
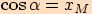 , pro každé
, pro každé 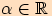 .
.
Jednotková kružnice s vyznačením funkcí sinus a kosinus
Poznámka. Funkce sinus a kosinus jsou definovány pomocí jednotkové kružnice, proto jsou nezávislé na volbě délkové jednotky.
Uvedenými definičními vztahy je každému číslu 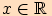 přiřazeno
právě jedno reálné číslo
přiřazeno
právě jedno reálné číslo 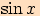 a právě jedno reálné číslo
a právě jedno reálné číslo
 ,
tj. tyto vztahy udávají funkční předpisy funkce sinus
,
tj. tyto vztahy udávají funkční předpisy funkce sinus 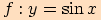 a funkce kosinus
a funkce kosinus  ,
, 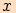 se nazývá argument funkce.
se nazývá argument funkce.
Souvislost jednotkové kružnice a grafu u funkce sinus
Souvislost jednotkové kružnice a grafu u funkce kosinus
Grafy funkcí sinus a kosinus argumentu 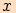 sestrojíme na základě jejich definice pomocí souřadnic bodů
sestrojíme na základě jejich definice pomocí souřadnic bodů 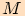 jednotkové kružnice
jednotkové kružnice 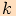 se středem v počátku
se středem v počátku 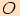 kartézské soustavy souřadnic.
kartézské soustavy souřadnic.
Graf funkce sinus se nazývá sinusoida a graf funkce
kosinus se nazývá kosinusoida . Přitom kosinusoida
je posunutá sinusoida o 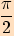 ve směru záporné poloosy
ve směru záporné poloosy
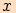 .
.
Definičním oborem funkcí sinus a kosinus je množina 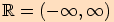 ,
proto na omezené nákresně můžeme zobrazit jen části jejich grafů.
,
proto na omezené nákresně můžeme zobrazit jen části jejich grafů.
Graf funkce sinus pro argument z intervalu
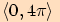
Graf funkce kosinus pro argument z intervalu
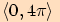
>>nahoru<<
Vlastnosti funkcí sinus a kosinus
Nejprve probereme podrobně každou vlastnost a na konci uvedeme shrnující tabulku.
Definiční obor obou funkcí je 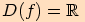 .
.
 Neexistuje
Neexistuje 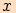 , ke kterému
bychom nepřiřadili žádnou funkční hodnotu.
, ke kterému
bychom nepřiřadili žádnou funkční hodnotu.
U obou funkcí to je interval 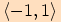 .
.
 Pro každé
Pro každé 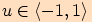 je přímka
je přímka
 sečnou nebo tečnou jednotkové kružnice.
Získáme tak vždy alespoň jeden bod kružnice, jehož první (druhá) souřadnice
je hodnotou funkce
sečnou nebo tečnou jednotkové kružnice.
Získáme tak vždy alespoň jeden bod kružnice, jehož první (druhá) souřadnice
je hodnotou funkce 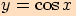 (
(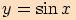 ) pro
některé
) pro
některé 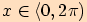 .
.
Je-li 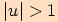 , pak je přímka o rovnici
, pak je přímka o rovnici
 vnější přímkou kružnice
vnější přímkou kružnice 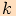 .
.
Z této vlastnosti funkce plyne také následující vlastnost.
Obě funkce jsou omezené zdola číslem 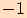 a shora číslem
a shora číslem
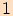 .
Tedy platí, že pro každé
.
Tedy platí, že pro každé 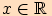 je
je
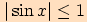 a
a
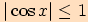 .
.
 Plyne to z jednotkové kružnice.
Plyne to z jednotkové kružnice.
Funkce sinus má maximum 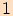 v bodech
v bodech
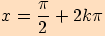 ,
minimum
,
minimum 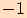 v bodech
v bodech
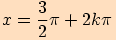 ,
kde
,
kde 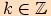 .
.
Funkce kosinus má maximum 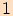 v bodech
v bodech
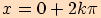 ,
minimum
,
minimum 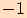 v bodech
v bodech 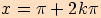 ,
kde
,
kde 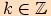 .
.
 Vše plyne z jednotkové kružnice.
Vše plyne z jednotkové kružnice.
Sinus je funce lichá a kosinus je funkce sudá.
Z definice liché funkce plyne 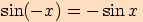 .
.
Z definice sudé funkce plyne 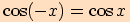 .
.
 Tyto vlastnosti můžeme snadno ověřit pomocí
jednotkové kružnice. Obě funkce jsou definovány na
Tyto vlastnosti můžeme snadno ověřit pomocí
jednotkové kružnice. Obě funkce jsou definovány na 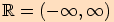 .
Také to můžeme poznat z grafů obou funkcí, graf funkce sinus je souměrný podle
počátku a graf funkce kosinus je souměrný podle osy
.
Také to můžeme poznat z grafů obou funkcí, graf funkce sinus je souměrný podle
počátku a graf funkce kosinus je souměrný podle osy 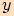 .
.

Obě jsou periodické, jejich nejmenší perioda je 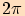 .
.
Tedy platí, že pro každé 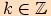 a pro každé
a pro každé
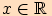
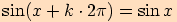
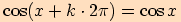
 Například je to vidět z grafů funkcí nebo z
jednotkové kružnice.
Například je to vidět z grafů funkcí nebo z
jednotkové kružnice.
Můžeme díky tomu zkoumat funkce 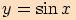 a
a
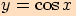 na intervalu
na intervalu 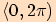 a popíšeme tak jejich chování na celém
a popíšeme tak jejich chování na celém 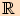 .
.

Funkce sinus je rostoucí v intervalech
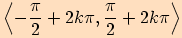 a klesající v intervalech
a klesající v intervalech 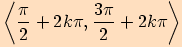 ,
kde
,
kde 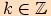 .
.
Funkce kosinus je rostoucí v intervalech 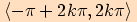 a klesající v intervalech
a klesající v intervalech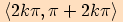 ,
kde
,
kde 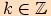 .
.
 Intervaly snadno určíme z grafů funkcí.
Intervaly snadno určíme z grafů funkcí.
Funkce sinus jich nabývá v bodech 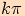 , tj.
, tj.
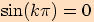 ,
, 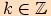 .
.
Funkce kosinus jich nabývá v bodech 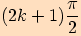 , tj.
, tj.
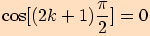 ,
,
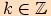 .
.
 Vyčteme to jednotkové kružnice.
Vyčteme to jednotkové kružnice.
Ty určíme nejlépe z grafů, jinak je lze vypočítat z příslušných goniometrických nerovností.
Funkce sinus má kladné hodnoty v intervalech 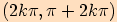 a záporné hodnoty v intervalech
a záporné hodnoty v intervalech 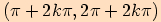 ,
,
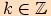 .
.
Funkce kosinus má kladné hodnoty v intervalech 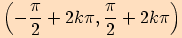 a záporné hodnoty v intervalech
a záporné hodnoty v intervalech 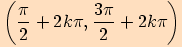 ,
,
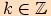 .
.
 Nejlépe je to vidět z grafů funkcí.
Nejlépe je to vidět z grafů funkcí.
Tabulka
Písmeno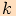 v tabulce označuje celé číslo.
v tabulce označuje celé číslo.
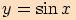 |
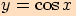 |
|
|---|---|---|
Definiční obor funkce 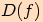 |
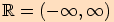 |
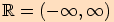 |
| Obor hodnot | 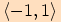 |
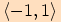 |
| Sudost,lichost funkce | lichá funkce | sudá funkce |
| Periodičnost funkce | periodická s periodou 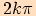 nejmenší perioda je 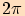 |
periodická s periodou 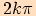 nejmenší perioda je 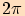 |
| Omezenost, neomezenost funkce |
omezená funkce | omezená funkce |
| Intervaly, v nichž je funkce rostoucí |
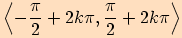 |
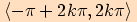 |
| Intervaly, v nichž je funkce klesající |
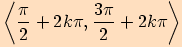 |
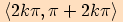 |
| Maximum funkce v bodě | 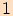 pro pro 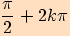 |
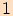 pro pro 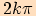 |
| Minimun funkce v bodě | 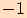 pro pro 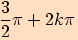 |
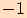 pro pro 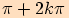 |
| Body,ve kterých jsou funční hodnoty nulové ( 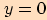 ) ) |
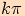 |
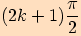 |
| Body,ve kterých jsou funční hodnoty kladné (  ) ) |
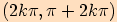 |
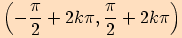 |
| Body,ve kterých jsou funční hodnoty záporné (  ) ) |
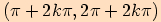 |
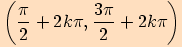 |
Příklady
1. a) Která z čísel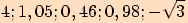 patří do oboru hodnot funkce
patří do oboru hodnot funkce 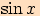 ?
?
 Obor hodnot funkce sinus je
Obor hodnot funkce sinus je
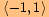 .
.
Čísla patřící do oboru hodnot jsou
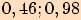

b) Která z čísel
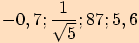 patří do oboru hodnot funkce
patří do oboru hodnot funkce  ?
?
 Obor hodnot funkce kosinus je
Obor hodnot funkce kosinus je
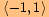 .
.
Výsledkem jsou hodnoty 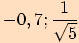

2.
Existuje 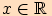 , pro něž je
, pro něž je
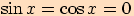 ?
?

že hledáme takové
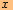 , aby se hodnoty obou
, aby se hodnoty oboufunkcí rovnaly
 .
. 
3. Dokažte, že platí:
a)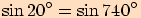

s nejmenšími periodami
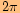 nebo
nebo
 a dále násobky,
a dále násobky,tudíž poté co uběhne tato perioda se funkční hodnoty opakují.
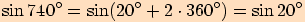

b)
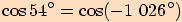

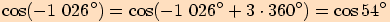

c)
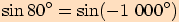

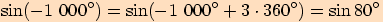

d)
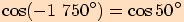



4.
Do kterého z intervalů 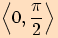 ,
, 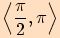 ,
,
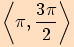 ,
, 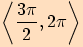 patří
patří
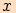 , pro něž je
, pro něž je
a) 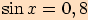 a zároveň
a zároveň
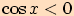

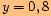 .
.Označíme průsečíky s jednotkovou kružnicí a spustíme kolmice a najdeme úsečky na ose
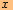 ,
,které odpovídají kosinu. Vybereme z nich tu, která je leží na záporné poloose.
Výsledkem je interval 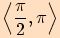 .
.

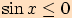 a zároveň
a zároveň
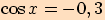 ?
? 
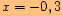 .
.Označíme průsečíky s jednotkovou kružnicí, spustíme kolmice a najdeme úsečky na ose
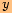 ,
,které odpovídají sinu. Vybereme z nich tu, která je leží na záporné poloose.
Výsledkem je interval 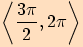 .
.

5.
Vypočítejte: 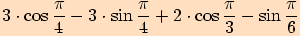

Najdeme je v kapitole Goniometrické funkce ostrého úhlu
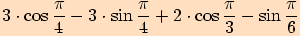 =
=
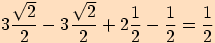

6.
Určete pomocí jednotkové kružnice všechna 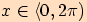 , pro která platí:
, pro která platí:
a) 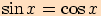

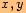 , tj. přímku
, tj. přímku  .
.Ta nám protne jednotkovou kružnici v bodech
 .
.Sestrojíme kolmice k oběma osám v těchto bodech.
Tedy výsledné body jsou
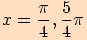

b)
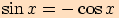

 nám protne jednotkovou kružnici v bodech
nám protne jednotkovou kružnici v bodech 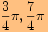 .
.Ověříme opět, že jsme dostali správný výsledek a to tak, že z obou bodů spustíme kolmice na obě osy.
Délky úseček odpovídající funkcím sinus a kosinus jsou stejně dlouhé, ale s jiným znaménkem.
Tedy výsledné body jsou
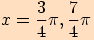

7.
Zapište množinu všech 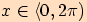 , pro která platí:
, pro která platí:
a) 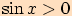 a zároveň
a zároveň
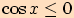
 Použijeme jednotkovou kružnici.
Použijeme jednotkovou kružnici.
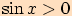 platí pro
platí pro
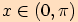

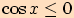 platí pro
platí pro
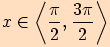

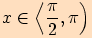

b) 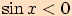 a zároveň
a zároveň
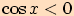

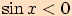 platí pro
platí pro
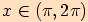

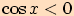 platí pro
platí pro
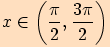

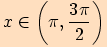 ,
,

8.
Určete definiční obory těchto funkcí:
a) 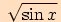

musí být větší nebo roven
 .
. 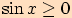

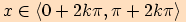

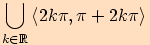

b)
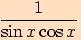

se nesmí rovnat
 .
. 

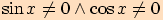

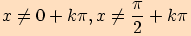

>>nahoru<<