Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Sinová věta
Pro každý trojúhelník 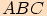 , jehož vnitřní úhly mají velikosti
, jehož vnitřní úhly mají velikosti
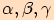 a strany délky
a strany délky 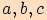 ,
platí
,
platí 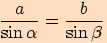 .
.
Sinová věta
Poznámka. Další vzorce vyplývají z principu cyklické záměny. Jsou
to tyto:
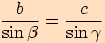
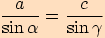
Sinovou větu můžeme také vyjádřit ve tvaru 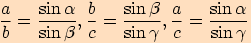 ,
,
tj. poměr délek dvou stran v trojúhelníku se rovná poměru velikostí sinů protilehlých úhlů
k těmto stranám.
Cyklická záměna
Důkaz
 Rozlišíme 3 typy trojúhelníků, ostroúhlý, pravoúhlý a tupoúhlý. Pro každý typ provedeme důkaz zvlášť. Úhel,
který budeme měřit, je u vrcholu
Rozlišíme 3 typy trojúhelníků, ostroúhlý, pravoúhlý a tupoúhlý. Pro každý typ provedeme důkaz zvlášť. Úhel,
který budeme měřit, je u vrcholu  , tedy úhel
, tedy úhel
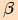 .
.
1) Úhel 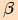 je ostrý, tj.
je ostrý, tj.
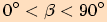 .
.
Nalezneme bod 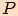 , který je patou kolmice
spuštěné z vrcholu
, který je patou kolmice
spuštěné z vrcholu 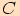 na stranu
na stranu 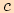 .
.
Vyjádříme velikost strany 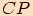 pomocí úhlu
pomocí úhlu 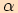 ,
,
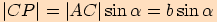 ,
,
a poté pomocí úhlu 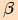 ,
, 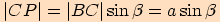 .
.
Nyní porovnáme výše uvedené vztahy 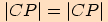 ,
tj.
,
tj.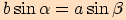 .
.
Tudíž 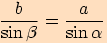 .
.
2) Úhel 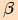 je pravý, tj.
je pravý, tj.
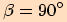 .
.
Bod 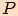 , který je patou kolmice nám splyne s bodem
, který je patou kolmice nám splyne s bodem
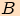 .
.
Důkaz provedeme obdobně, ale musíme si uvědomit, že 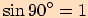 ( viz Určování hodnot
goniometrických funkcí).
( viz Určování hodnot
goniometrických funkcí).
Vyjáříme také velikost úsečky 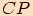 nejprve pomocí
úhlu
nejprve pomocí
úhlu 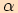 ,
, 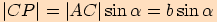 ,
,
a potom pomocí úhlu 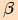 ,
, 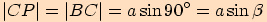 .
.
Závěrem získáme rovnost 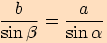 .
.
3) Úhel 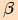 je tupý, tj.
je tupý, tj.
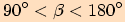 .
.
Také nejprve nalezneme bod  a vyjádříme velikost
úsečky
a vyjádříme velikost
úsečky 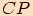 dvojím způsobem
dvojím způsobem
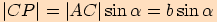
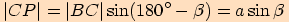 .
.
Musíme si uvědomit, že platí rovnost 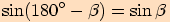 ( viz Vzorce pro goniometrické funkce.)
( viz Vzorce pro goniometrické funkce.)
Nakonec opět porovnáme obě vyjádření a vyjde nám vztah
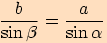 .
.
Cyklickou záměnou dostaneme další vyjádření. Tím je důkaz u konce.
>>nahoru<<
Příklady
1.
Určete velikosti všech vnitřních úhlů a stran v trojúhelníku 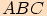 ,
jestliže
,
jestliže 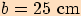 ,
, 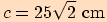 ,
,
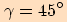 .
.

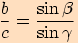

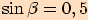

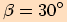

 dopočítáme z toho, že součet úhlů v trojúhelníku je
dopočítáme z toho, že součet úhlů v trojúhelníku je  .
.
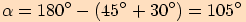

 vypočítáme pomocí sinové věty.
vypočítáme pomocí sinové věty.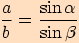

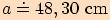

2.
Trojúhelník  má strany
má strany 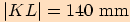 ,
,
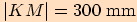 a
velikost úhlu
a
velikost úhlu 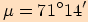 .
Vypočítejte velikosti ostatních úhlů a strany.
.
Vypočítejte velikosti ostatních úhlů a strany.

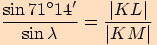

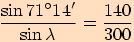

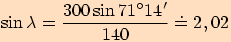
Úloha nemá řešení, protože nám sinus vyšel větší než
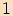 a to nelze (viz kapitola Sinus a kosinus)
a to nelze (viz kapitola Sinus a kosinus) 
>>nahoru<<