\begin{align}
\end{align}
Důkazy pravidel derivování II
V této podkapilole dokážeme pravidla pro derivování následujících elementárních funkcí:
- \(y = \sin{x}\);
- \(y = \cos{x}\);
- \(y = a^x\), kde \(a \in \mathbb R^{+}\).
Pro funkci \(f : y = \sin{x}\), \(x \in \mathbb R\), platí \(y^{\prime} = \cos{x}\).
Důkaz
Při důkazu se využijí vztahy
\(\sin{\alpha} - \sin{\beta} \; = \; 2\cos{\Large\frac{\alpha+\beta}{2}} \sin{\Large\frac{\alpha-\beta}{2}}, \; \; {\Large\lim\limits_{x \to 0}}{\Large\frac{\sin{x}}{x}} \; = \; 1\).
Víme, že
\(y^{\prime}\normalsize\; = \; \Large\lim\limits_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}\normalsize\; = \; \Large\lim\limits_{\Delta x \to 0} \frac{\sin(x+\Delta x) - \sin{x}}{\Delta x}\).
S použitím uvedených vztahů přepíšeme limitu na
\(\Large\lim\limits_{\Delta x \to 0} \LARGE\frac{2 \cos{\frac{x+\Delta x + x}{2}} \sin{\frac{x+\Delta x - x}{2}} }{\Delta x} \normalsize \; = \; \Large\lim\limits_{\Delta x \to 0} \LARGE\frac{2 \cos(x+\frac{\Delta x}{2}) \sin{\frac{\Delta x}{2}} }{\Delta x} \normalsize \; =\)
\(= \; \Large\lim\limits_{\Delta x \to 0} \normalsize [ \cos(x + {\Large\frac{\Delta x}{2}})\LARGE\frac{\sin{\frac{\Delta x}{2}} }{\frac{\Delta x}{2}}\normalsize] \; = \; [\Large\lim\limits_{\Delta x \to 0} \normalsize \cos(x + {\Large\frac{\Delta x}{2}}) \normalsize ] \cdot [\Large\lim\limits_{\Delta x \to 0} \LARGE\frac{\sin{\frac{\Delta x}{2}} }{\frac{\Delta x}{2}}\normalsize ] \; = \)
\(= \; \cos(x)\cdot 1 \; = \; \cos{x}\)
Poznámka k hodnotě limity \({\Large\lim\limits_{x \to 0}}{\Large\frac{\sin{x}}{x}}.\) 
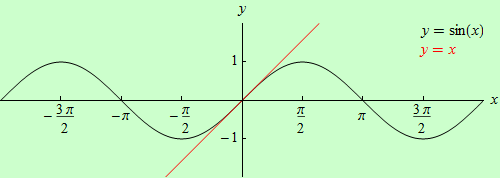
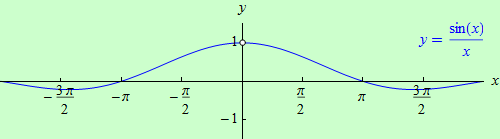
To, že má tato limita hodnotu jedna, nelze středoškolskými matematickými prostředky dokázat. Na následujícím obrázku jsou zobrazeny grafy funkcí \(y = \sin{x}\) (černý) a \(y = x\) (červený). Na obrázku pod ním je zobrazen graf funkce \(y = \Large\frac{\sin{x}}{x}\), z něhož je patrná hodnota limity v bodě \(x = 0\).
Pro funkci \(f : y = \cos{x}\), \(x \in \mathbb R\), platí \(y^{\prime} = -\sin{x}\).
Důkaz
Při důkazu se využijí vztahy
\(\cos{\alpha} - \cos{\beta} \; = \; -2\sin{{\Large\frac{\alpha+\beta}{2}}} \sin{{\Large\frac{\alpha-\beta}{2}}}, \; \; {\Large\lim\limits_{x \to 0}}{\Large\frac{\sin{x}}{x}} \; = \; 1\).
Víme, že
\(y^{\prime}\normalsize\; = \; \Large\lim\limits_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}\normalsize\; = \; \Large\lim\limits_{\Delta x \to 0} \frac{\cos(x+\Delta x) - \cos{x}}{\Delta x}\).
S použitím uvedených vztahů přepíšeme limitu na
\(\Large\lim\limits_{\Delta x \to 0} \LARGE\frac{-2 \sin{\frac{x+\Delta x + x}{2}} \sin{\frac{x+\Delta x - x}{2}} }{\Delta x} \normalsize \; = \; \Large\lim\limits_{\Delta x \to 0} \LARGE\frac{-2 \sin(x+\frac{\Delta x}{2}) \sin{\frac{\Delta x}{2}} }{\Delta x} \normalsize \; =\)
\(= \; \Large\lim\limits_{\Delta x \to 0} \normalsize [ -\sin(x + {\Large\frac{\Delta x}{2}})\LARGE\frac{\sin{\frac{\Delta x}{2}} }{\frac{\Delta x}{2}}\normalsize] \; = \; [\Large\lim\limits_{\Delta x \to 0} \normalsize -\sin(x + {\Large\frac{\Delta x}{2}})] \cdot [\Large\lim\limits_{\Delta x \to 0} \LARGE\frac{\sin{\frac{\Delta x}{2}} }{\frac{\Delta x}{2}}\normalsize] \; =\)
\(= \; -\sin(x) \cdot 1 \; = \; -\sin{x}\)
Poznámka k hodnotě limity \({\Large\lim\limits_{x \to 0}}{\Large\frac{\sin{x}}{x}}\) je uvedena u důkazu derivace funkce sinus.
Jestliže existují \(u^{\prime}(v(x))\) a \(v^{\prime}(x)\), pak: \([u(v(x))]^{\prime} \; = \; u^{\prime}(v(x))\cdot v^{\prime}(x)\).
Bez důkazu
Důkaz svou náročností přesahuje možnosti tohoto webu. Lze ho najít v Jarníkovi [2] na stránkách 217 až 219.
Pro funkci \(f : y = a^x\), \(x \in \mathbb R\), \(a \in \mathbb R^{+}\), platí \(y^{\prime} = a^x\ln{a}\).
Poznámka: Všimněte si, že když se základ \(a\) rovná Eulerovu číslu \(e\), tak \(\ln{a} = \ln{e} = 1\). Derivace pak odpovídá derivaci funkce \(y = e^x\).
Důkaz
Při důkazu se využije pravidlo pro derivaci složené funkce a vztah
\(a^x \; = \; (e^{\ln{a}})^x \; = \; e^{x\ln{a}}\).
Víme, že
\(y^{\prime} \; = \; (a^x)^{\prime} \; = \; (e^{x\ln{a}})^{\prime} \; = \; [u(v(x))]^{\prime}\),
kde \(u(x) = e^x\) a \(v(x) = x\ln{a}\). Platí, že \(u^{\prime}(x) = u(x)\).
Využijeme pravidlo pro derivaci složené funkce a dostaneme
\(u^{\prime}(v(x))\cdot v^{\prime}(x) \; = \; u(v(x))\cdot (x\ln{a})^{\prime} \; = \; e^{x\ln{a}}\cdot \ln{a} \; = \; a^x\ln{a}\)