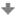Příklad 1: Cesta na staveniště
Staveniště v bodě \(A\) je vzdáleno 4 km od bodu \(B\) ležícího na silnici vedoucí do překladiště stavebního materiálu v bodě \(C\). Délka silnice z bodu \(B\) do bodu \(C\) je 6 km. Úsečky \(BA\) a \(BC\) svírají pravý úhel. Ze silnice je třeba vybudovat přímou provizorní cestu na staveniště. Náklady na přepravu materiálů po silnici jsou 3 Kč/km. Náklady na přepravu materiálů po provizorní cestě jsou 5 Kč/km.
Ve kterém místě na silnici je třeba vybudovat odbočku na provizorní cestu, aby celková cena za přepravu z překladiště stavebního materiálu v bodě \(C\) do staveniště v bodě \(A\) byla nejnižší, a jaká cena to bude? Situace je znázorněna v následujícím apletu.
Řešení
Odbočku ze silnice na provizorní cestu označíme jako bod \(D\).
1. Nejdříve identifikujeme proměnnou, jejíž extrém budeme hledat, a typ extrému (maximum nebo minimum).
Minimalizujeme cenu přepravy. Označme tuto proměnnou písmenem \(c\) (jako cena).
Délka úsečky \(BD\) v km je \(x.\).
Délka úsečky \(AD\) v km je \(\sqrt{|AB|^2+|BD|^2} = \sqrt{16+x^2}.\)
Cena za přepravu pro úsečce \(AD\) v Kč je \(5\sqrt{16+x^2}.\)
Délka úsečky \(DC\) v km je \(|BC| - |BD| = 6-x.\)
Cena za přepravu pro úsečce \(DC\) v Kč je \(3(6-x).\)
Celková cena za přepravu v Kč je
\(c = 5\sqrt{16+x^2} + 3(6-x).\)
2. Ze vztahů mezi proměnnými docílíme jejich redukce tak, aby proměnná, jejíž extrém hledáme, závisela jen na jedné nezávislé proměnné.
Zde nemusíme nic redukovat, neboť proměnná \(c\) závisí pouze na proměnné \(x.\)
3. Dále určíme definiční obor nezávislé proměnné \(x\), na níž závisí proměnná \(c\), jejíž extrém hledáme.
Je zřejmé, že definiční obor proměnné \(x\) je
\(x \in \langle 0, 6 \rangle\).
4. Nyní přepíšeme vztah \(c = 5\sqrt{16+x^2} + 3(6-x)\) pro \(x \in \langle 0, 6 \rangle\) do tvaru funkčního předpisu. Místo proměnné \(c\) napíšeme \(f(x)\). Z definičního oboru proměnné \(x\) stanovíme definiční obor funkce \(f.\)
\(f(x) = 5\sqrt{16+x^2} + 3(6-x)\) s definičním oborem \(D(f) = \langle 0, 6 \rangle.\)
5. Najdeme hledaný extrém.
Hledáme globální minimum. Platí, že \(f^{\prime}(x) = -3+\dfrac{5x}{\sqrt{16+x^2}}.\)
Vzhledem k tomu, že funkce \(f\) má definovanou derivaci na celém intervalu \(( 0, 6 )\), tak body „podezřelými z extrému“ jsou pouze stacionární body funkce \(f\) a krajní body intervalu \(\langle 0, 6 \rangle\), tj. \(x = 0\) a \(x = 6\).
Stacionární body splňuji rovnici \(-3+\dfrac{5x}{\sqrt{16+x^2}} = 0\). Řešením z definičního oboru funkce \(f\) je
\(x = 3.\)
Ověříme, zda má funkce \(f\) ve stacionárním bodě \(x = 3\) globální minimum.
Funkce \(f\) je na intervalu \(\langle 0, 6 \rangle\) spojitá. Její derivace je na intervalu \(( 0, 6 )\) všude definovaná. Navíc tam má funkce \(f\) jediný stacionární bod \(x = 3\). Proto přicházejí v úvahu pouze tyto možnosti:
(a) funkce \(f\) je na intervalu \(\langle 0, 3 \rangle\) klesající a na intervalu \(\langle 3, 6 \rangle\) rostoucí;
(b) funkce \(f\) je na intervalu \(\langle 0, 3 \rangle\) rostoucí a na intervalu \(\langle 3, 6 \rangle\) klesající;
(c) funkce \(f\) je na intervalu \(\langle 0, 6 \rangle\) buď jen rostoucí, nebo jen klesající.
Přitom jsme využili teorii z kapitoly Monotónnost a extrémy, podkapitoly Monotónnost tabulkovou metodou.
Určíme hodnoty funkce \(f\) v bodech \(x = 0\), \(x = 3\) a \(x = 6\):
\(f(0) = 38\);
\(f(3) = 34\);
\(f(6) \doteq 36{,}06\).
Vidíme, že nemohou platit možnosti (b) a (c). Musí tedy platit možnost (a). To znamená, že funkce \(f\) má v bodě \(x = 3\) globální minimum.
6. Zapíšeme řešení.
Celková cena za přepravu bude nejnižší pro \(x = 3\) km a činí \(f(3) = 34\) Kč.
Odkazy na příklady